Prolog Tutorial -- 5.3

5.3 α&beta search in Prolog, tic tac toe example

This section adapts the α&beta search framework in The Art of Prolog, by L. Sterling and E. Shapiro (1986) for playing the game of tic tac toe (noughts and crosses). One purpose is to study that framework by testing the adaptation to the TicTacToe game. Another intended purpose is to have a Prolog tic tac toe expert agent that can play against the GUI interface developed in Section 8.4.

representing the tic tac toe board in Prolog

To represent the tictactoe board we use a Prolog list. The empty board, before play starts is

_|_|_
_|_|_   ~ [_Z1,_Z2,_Z3,_Z4,_Z5,_Z6,_Z7,_Z8,_Z9]
_|_|_      | 1st row  |  2nd row  | third row |

After playing two moves each, here is another board ...

o|_|_
o|x|x   ~ [o,_Z2,_Z3,o,x,x,_Z7,_Z8,_Z9]
_|_|_

The reason for this somewhat obscure representation is so as to avoid having to process a list representation for the board. Instead, a player marks the board by binding a free variable.

:- dynamic board/1.
:- retractall(board(_)).
:- assert(board([_Z1,_Z2,_Z3,_Z4,_Z5,_Z6,_Z7,_Z8,_Z9])). 

%%%%%
%%  Generate possible marks on a free spot on the board.
%%  Use mark(+,+,-X,-Y) to query/generate possible moves (X,Y).
%%%%%
mark(Player, [X|_],1,1) :- var(X), X=Player.
mark(Player, [_,X|_],2,1) :- var(X), X=Player.
mark(Player, [_,_,X|_],3,1) :- var(X), X=Player.
mark(Player, [_,_,_,X|_],1,2) :- var(X), X=Player.
mark(Player, [_,_,_,_,X|_],2,2) :- var(X), X=Player.
mark(Player, [_,_,_,_,_,X|_],3,2) :- var(X), X=Player.
mark(Player, [_,_,_,_,_,_,X|_],1,3) :- var(X), X=Player.
mark(Player, [_,_,_,_,_,_,_,X|_],2,3) :- var(X), X=Player.
mark(Player, [_,_,_,_,_,_,_,_,X|_],3,3) :- var(X), X=Player.

%%%%%
%%  Record a move: record(+,+,+).
%%%%%
record(Player,X,Y) :- 
   retract(board(B)), 
   mark(Player,B,X,Y),
   assert(board(B)).

For example, after this code is loaded, consider the following goal ...


?- board(B),mark(o,B,X,Y).
B = [o, _G286, _G289, _G292, _G295, _G298, _G301, _G304, _G307] X = 1 Y = 1 ;
B = [_G283, o, _G289, _G292, _G295, _G298, _G301, _G304, _G307] X = 2 Y = 1 ;
B = [_G283, _G286, o, _G292, _G295, _G298, _G301, _G304, _G307] X = 3 Y = 1 ;
B = [_G283, _G286, _G289, o, _G295, _G298, _G301, _G304, _G307] X = 1 Y = 2 ;
B = [_G283, _G286, _G289, _G292, o, _G298, _G301, _G304, _G307] X = 2 Y = 2 ;
B = [_G283, _G286, _G289, _G292, _G295, o, _G301, _G304, _G307] X = 3 Y = 2 ;
B = [_G283, _G286, _G289, _G292, _G295, _G298, o, _G304, _G307] X = 1 Y = 3 ;
B = [_G283, _G286, _G289, _G292, _G295, _G298, _G301, o, _G307] X = 2 Y = 3 ;
B = [_G283, _G286, _G289, _G292, _G295, _G298, _G301, _G304, o] X = 3 Y = 3 ;
No

This illustrates that all the moves can be be generated by backtracking on the mark clauses. Now, let's first record an xin the center and then generate all possible subsequent moves for o ...


?- record(x,1,1), board(B), findall((X,Y),mark(o,B,X,Y),Moves).

B = [x, _G370, _G373, _G376, _G379, _G382, _G385, _G388, _G391]
X = _G186
Y = _G187
Moves = [ (2, 1), (3, 1), (1, 2), (2, 2), (3, 2), (1, 3), (2, 3), (3, 3)] 

Yes
?- board(B).

B = [x, _G234, _G237, _G240, _G243, _G246, _G249, _G252, _G255] 

Yes

Notice carefully that record does in fact record (assert) a move, but that mark simply finds all possible moves(without actually recording them).

We need an evaluation function that measures how good a board is for a player. We use the well known one that measures the difference between the open lines of play for each player,

value(Board) = (# open lines for o - # open lines for x)

Larger values favor o, smaller values favor x. Our champion is o (computer) whose algorithms below will search to maximixe a move's value. The algoritms assume that x would search to minimize value. A winning board for o has value 100, a winning board for x has value -100.


%%%%%
%% Calculate the value of a position, o maximizes, x minimizes.
%%%%%
value(Board,100) :- win(Board,o), !.
value(Board,-100) :- win(Board,x), !.
value(Board,E) :- 
   findall(o,open(Board,o),MAX), 
   length(MAX,Emax),      % # lines open to o
   findall(x,open(Board,x),MIN), 
   length(MIN,Emin),      % # lines open to x
   E is Emax - Emin.


%%%%% 
%%  A winning line is ALREADY bound to Player. 
%%  win(+Board,+Player) is true or fail.
%%    e.g., win([P,P,P|_],P).  is NOT correct, because could bind 
%%%%%
win([Z1,Z2,Z3|_],P) :- Z1==P, Z2==P, Z3==P.
win([_,_,_,Z1,Z2,Z3|_],P) :-  Z1==P, Z2==P, Z3==P.
win([_,_,_,_,_,_,Z1,Z2,Z3],P) :-  Z1==P, Z2==P, Z3==P.
win([Z1,_,_,Z2,_,_,Z3,_,_],P) :-  Z1==P, Z2==P, Z3==P.
win([_,Z1,_,_,Z2,_,_,Z3,_],P) :-  Z1==P, Z2==P, Z3==P.
win([_,_,Z1,_,_,Z2,_,_,Z3],P) :-  Z1==P, Z2==P, Z3==P.
win([Z1,_,_,_,Z2,_,_,_,Z3],P) :-  Z1==P, Z2==P, Z3==P.
win([_,_,Z1,_,Z2,_,Z3,_,_],P) :-  Z1==P, Z2==P, Z3==P.

%%%%%
%%  A line is open if each position is either free or equals the Player
%%%%%
open([Z1,Z2,Z3|_],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([_,_,_,Z1,Z2,Z3|_],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([_,_,_,_,_,_,Z1,Z2,Z3],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([Z1,_,_,Z2,_,_,Z3,_,_],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([_,Z1,_,_,Z2,_,_,Z3,_],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([_,_,Z1,_,_,Z2,_,_,Z3],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([Z1,_,_,_,Z2,_,_,_,Z3],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).
open([_,_,Z1,_,Z2,_,Z3,_,_],Player) :- (var(Z1) | Z1 == Player),(var(Z2) | Z2 == Player), (var(Z3) | Z3 == Player).

%%%%%
%% Calculate the value of a position, o maximizes, x minimizes.
%%%%%
value(Board,100) :- win(Board,o), !.
value(Board,-100) :- win(Board,x), !.
value(Board,E) :- 
   findall(o,open(Board,o),MAX), 
   length(MAX,Emax),      % # lines open to o
   findall(x,open(Board,x),MIN), 
   length(MIN,Emin),      % # lines open to x
   E is Emax - Emin.

For example,

?- value([_X,o,o,_Y,o,x,x,_Z,x],V).
V = 0

The reader should try several example boards, and also compute the value by inspection.

adapting αβ search for tic tac toe

The αβ search algorithm looks ahead in order to calculate what move will be best for a player. The algorithm maximizes the value for o, and minimizes the value for x. Here is the basic code framework ...


alpha_beta(Player,0,Position,_Alpha,_Beta,_NoMove,Value) :- 
   value(Position,Value).

alpha_beta(Player,D,Position,Alpha,Beta,Move,Value) :- 
   D > 0, 
   findall((X,Y),mark(Player,Position,X,Y),Moves), 
   Alpha1 is -Beta, % max/min
   Beta1 is -Alpha,
   D1 is D-1, 
   evaluate_and_choose(Player,Moves,Position,D1,Alpha1,Beta1,nil,(Move,Value)).

evaluate_and_choose(Player,[Move|Moves],Position,D,Alpha,Beta,Record,BestMove) :-
   move(Player,Move,Position,Position1), 
   other_player(Player,OtherPlayer),
   alpha_beta(OtherPlayer,D,Position1,Alpha,Beta,_OtherMove,Value),
   Value1 is -Value,
   cutoff(Player,Move,Value1,D,Alpha,Beta,Moves,Position,Record,BestMove).
evaluate_and_choose(_Player,[],_Position,_D,Alpha,_Beta,Move,(Move,Alpha)).

cutoff(_Player,Move,Value,_D,_Alpha,Beta,_Moves,_Position,_Record,(Move,Value)) :- 
   Value >= Beta, !.
cutoff(Player,Move,Value,D,Alpha,Beta,Moves,Position,_Record,BestMove) :- 
   Alpha < Value, Value < Beta, !, 
   evaluate_and_choose(Player,Moves,Position,D,Value,Beta,Move,BestMove).
cutoff(Player,_Move,Value,D,Alpha,Beta,Moves,Position,Record,BestMove) :- 
   Value =< Alpha, !, 
   evaluate_and_choose(Player,Moves,Position,D,Alpha,Beta,Record,BestMove).

other_player(o,x).
other_player(x,o).

To test the code from the Prolog command line, we add a few instructions ...

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%% For testing, use h(+,+) to record human move,
%%% supply coordinates. Then call c (computer plays).
%%% Use s to show board.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
h(X,Y) :- record(x,X,Y), showBoard.

c :- 
   board(B), 
   alpha_beta(o,2,B,-200,200,(X,Y),_Value), % <=== NOTE
   record(o,X,Y), showBoard.

showBoard :- 
   board([Z1,Z2,Z3,Z4,Z5,Z6,Z7,Z8,Z9]), 
   write('    '),mark(Z1),write(' '),mark(Z2),write(' '),mark(Z3),nl,
   write('    '),mark(Z4),write(' '),mark(Z5),write(' '),mark(Z6),nl,
   write('    '),mark(Z7),write(' '),mark(Z8),write(' '),mark(Z9),nl.
s :- showBoard.

mark(X) :- var(X), write('#').
mark(X) :- \+var(X),write(X).

Now, consider the following interactions ...

?- s.           % show the board
    # # #
    # # #
    # # #

Yes
?- h(2,1).      % Human marks x at 2,1 (not best)
    # x #
    # # #
    # # #

Yes
?- c.           % computer thinks, moves to 2,2
    # x #
    # o #
    # # #

Yes
?- h(1,1).      %  Human moves to 1,1
    x x #
    # o #
    # # #

Yes
?- c.           % computer's move. SEE ANALYSIS BELOW 
    x x o
    # o #
    # # #

... etc.

... a cat's game.

The Prolog program has been designed so that the state of the tic tac toe board is stored after each board, rather than a continuing program that alternately interacts with the players. The reason for this design choice is that we will connect the Prolog tic tac toe player up with a Java GUI in Section 8.4. The Java program will also store the state of the current board. In this way, Prolog and Java will merely have to communicate with each other by telling the other player what the move is: a pair of numbers X,Y.

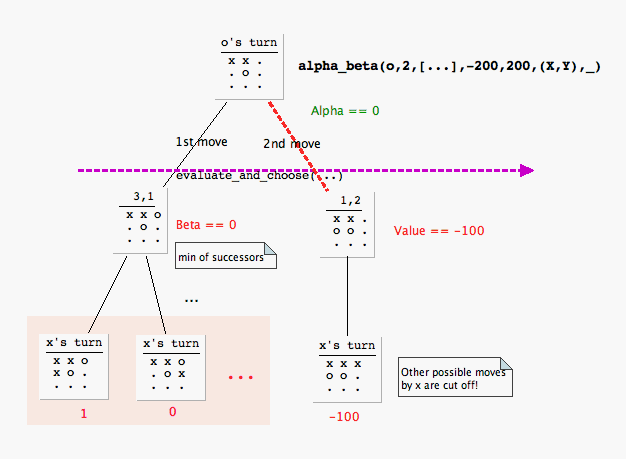
Let us look at what happens when Prolog computes the last move shown in the game above. The following diagram graphically illustrates what happens for o's choices other than the first possible (and critically best) move. All of the moves are expanded in the order generated by the program. The second possible move [x,x,_,o,o,_,_,_,_] gives x the opportunity to choose her win [x,x,x,o,o,_,_,_,_]. Our maximizer, o, will not tolerate this and searches no further. The α-cutoff is the red dashed edge from the root to the second tier choice: Notice that cuttoff is called by evaluate_and_choose, which can thus truncate the possibities! The backed-up value Alpha == 0 was obtained from the leftmost search: The best that o can be guarateed from the ist move.

Fig. 5.3

The αβ algorithm brings much more power to bear than is be actually needed to play tic tac toe.

The real advantage that αβ search brings to a more complex game derives from its ability to cutoff the search tree for search which looks ahead by many more moves. Sterling and Shapiro (1986) provide an example for the game of Kalah. The complexity of Kalah takes better advantage of αβ search, and so too can other more complicated games.

It is possible that future versions of the Prolog Tutorial will study more complex games.

The reference Principles of Artificial Intelligence by Nilsson (1980) has a nice discussion of αβ search, and uses tic tac toe as a motivating example.

Prolog Code for tic tac toe discussed in this section.
Prolog Tutorial Contents