3.2 Cut

The cut goal succeeds whenever it is the current goal, AND the derivation tree is trimmed of all other choices on the way back to and including the point in the derivation tree where the cut was introduced into the sequence of goals.

For the previous derivation tree, this means that the branches labeled #2 and #3 are eliminated, and hence the entire subtrees below these two edges are also cut off. This then corresponds to only producing the first answer X=a:

?- p(X),!.
X=a ;
no

?- r(X),!,s(Y).
X=a Y=a ;
X=a Y=b ;
X=a Y=c ;
no

?- r(X), s(Y), !.
X=a Y=a ;
no

as expected.

Suppose that a cut occurs in the body of the program. The cut rule (above) still applies when the cut appears as a called subgoal. The cut is used in the body of a given clause so as to avoid using clauses appearing after the given clause in the program. To illustrate, consider the following program:

part(a). part(b). part(c).
red(a). black(b).
color(P,red) :- red(P),!.
color(P,black) :- black(P),!.
color(P,unknown).

A derivation tree for goal ?- color(a,C) is

Fig. 3.2.1

which corresponds with

?- color(a,C).
C = red

Fig. 3.2.2

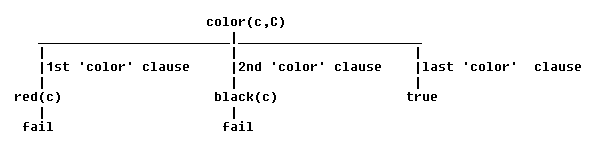
which corresponds with

?- color(c,C).
C = unknown

The Prolog cut is a procedural device for controlling goal satisfaction. The use of cut affects the meanings of programs. For example, in the 'color' program, the following program clause tree says that 'color(a,unknown)' should be a consequence of the program:

Fig. 3.2.3

The cut in the program enables Prolog to "avoid" this answer. It would be difficult to modify the program clause tree definition (for program consequences) to reflect the procedural meaning of cut. However, program clause trees can still be useful to diagram answers that could result without the cut.

Exercise 3.2.1 (a) What happens if one were to use the (suspect) program

max(X,Y,Y) :- Y>X, !.
max(X,Y,X).

What can happen for goal ?-max(1,2,1), for example? Use a clause tree to show that 'max(1,2,1)' is a consequence of the program as it stands. What assumption must one make in order for this Prolog specification to correctly compute the maximum of two numbers?

Exercise 3.2.2 Suppose that, in program P of section 3.1, clause #2 is changed so that it reads

p(X) :- q(X), !, r(X).

What answers can now be produced by the goal ?-p(X)? Why? Show why using the Prolog derivation tree (modified to suit the new rule).

The best use of cut is as an efficiency device, to avoid additional computations that are not desired or required in a program. A use of a cut which only improves efficiency is referred to as a green cut. A good example of a green cut is in the definition of the predicate 'is_same-level_as' in section 2.5. Otherwise the use is a red cut. The use of the cut in the 'color' program is red (pun intended), but the cut was used to restrict answers -- that is, block what would otherwise be reported as consequences of the program. Here is another version of 'color', using Prolog's implication '->':

color(X,C) :- red(X) -> C = red
                ;
              black(X) -> C = black
                ; 
              C = unknown.