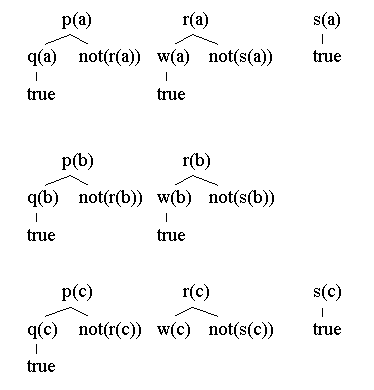
Fig. 2.5
not(P) :- call(P), !, fail.The goal ?-call(P) forces an attempt to satisfy the goal P. Most Prolog interpreters have a built-in version of this predicate. Quintus, SWI, and many other prologs use '\+' rather than 'not'.
not(P).
Section 3.2 has a discussion of the Prolog cut predicate '!'.
Another way one can write the 'not' definition is using the Prolog implication operator '->' :
not(P) :- (call(P) -> fail ; true)
The body can be read "if call(P) succeeds (i.e., if P succeeds as a goal) then fail, otherwise succeed". The semicolon ';' appearing here has the meaning of exclusive logical-or.
There will be numerous uses of 'not' in subsequent programs in the chapter.
It is important to realize that in a goal ?-not(g), if g has variables, and some instance of these variables lead to satisfaction of g, then ?-not(g) fails. For example, consider the following 'bachelor program:
bachelor(P) :- male(P), not(married(P)).
male(henry).
male(tom).
married(tom).
Then
?- bachelor(henry).
yes
?- bachelor(tom).
no
?- bachelor(Who).
Who= henry ;
no
?- not(married(Who)).
no.
The first three responses are correct and as expected. The answer to the fourth query might have been unexpected at first. But consider that the goal ?-not(married(Who)) fails because for the variable binding Who=tom, married(Who) succeeds, and so the negative goal fails. Thus, negative goals ?-not(g) with variables cannot be expected to produce bindings of the variables for which the goal g fails.
The definition of program clause tree in previous sections was intended for programs without negation as failure. For programs having negation as failure in the bodies of program clauses, the definition of a program clause tree, and the definition of a consequence based upon these trees needs to be carefully formulated. We will illustrate this aspect with some carefully chosen examples (and three exercises) below.
For example, consider the program
p(X) :- q(X), not(r(X)).
r(X) :- w(X), not(s(X)).
q(a). q(b). q(c).
s(a). s(c).
w(a). w(b).
Consider the following three sets of clause trees.
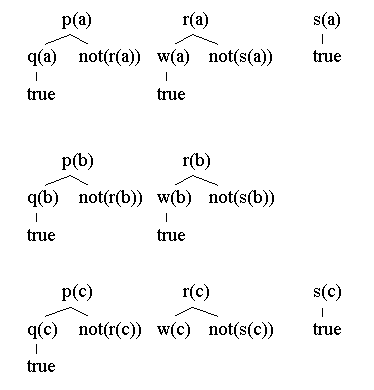
Now, the first set (across) is used to show that p(a) is a consequence of the program, the second set can be used to show that p(b) is not a consequence the program, and the third set shows that p(c) is a consequence of the program. Notice that the clause trees are now drawn so that negative nodes 'not(g)' are leaves, and new trees rooted at g are investigated.
Exercise 2.5.1 Load the sample program into Prolog and verify that Prolog will compute answers in accordance with our determination of consequences.
Exercise 2.5.2 Consider the following modification of the sample program.
p(X) :- q(X), not(r(X)).
r(X) :- w(x), not(s(X)).
q(a). q(b). q(c).
s(a) :- p(a). s(c).
w(a). w(b).
What happens now if one tries to argue whether or not p(a) is a consequence of this program? This shows that difficulties are encountered if there is recursion through negation. What happens if we allow Prolog to try the goal ?-p(a). ?
Exercise 2.5.3 Consider the following program.
u(X) :- not(s(X)).
s(X) :- s(f(X)).
What happens with this example if one tries to determine consequences based upon clause trees? What does Prolog do when given the goal ?-u(1). ? Is s(1) a consequence of the program?
The last two exercises show that programs with negation as failure can be problematic if there is either recursion through negation or if the negation of some unbounded literal is considered.