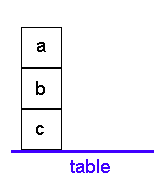
Fig. 2.19.1
In this section we present a simplified approach to generating plans of action for a hypothetical robot. The basic situation involves boxes on a table. Individual boxes are either on the table or can be stacked on top of other boxes. Only one box will fit directly on top of another box, and boxes may not overlap one another. The robot is assumed to be capable of moving only one box at a time, so to move a particular box which has other boxes stacked on top of it, the robot must first unstack the boxes until the particular box has a clear top.

The situation depicted in the picture will be represented by the following clauses:
on(a,b). on(b,c). on(c,table).
We could think of the part of our program giving the definition of 'on' as a kind of "blackboard" where the current state of the blocks world is recorded. The rest of the program will involve rules for how to accomplish various tasks involving the blocks world. As rearrangement goals are satisfied, changes will be made to the world-state blackboard, using assert, and retract. For example, if block a is moved from the top of b to the table, this would amount to retracting 'on(a,b)' and asserting 'on(a,table)'.
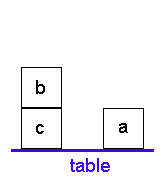
on(a,table). on(b,c). on(c,table).
We will record this action by asserting 'move(a,b,table)' into the program. The part of the program defining 'move' will be the "action blackboard" recording a plan. Here is a non- recursive action specification regarding how to put one block onto another:
put_on(A,B) :-
A \== table,
A \== B,
on(A,X),
clear(A),
clear(B),
retract(on(A,X)),
assert(on(A,B)),
assert(move(A,X,B)).
clear(table).
clear(B) :-
not(on(_X,B)).
This action specification has the form
action :- preconditions,
retract(affected_old_properties),
assert(new_properties).
In a nonrecursive action specification, the preconditions will not themselves contain other actions. Thus, in the example so far,
?- put_on(a,table). yes ?- listing(on), listing(move). on(b,c). on(c,table). on(a,table). move(a,b,table). yes ?- put_on(c,a). no
The last goal fails since a block must have a clear top in order to be moved. Thus
?- put_on(b,table), put_on(c,a). yes
is successful because b is moved off of c before c is moved to the top of a. Note well that action specifications do not change properties that are not affected by the action, because unaffected properties are not retracted. The task of capturing this desired behavior is called the frame problem.
Here is a recursive action specification for moving blocks:
r_put_on(A,B) :-
on(A,B).
r_put_on(A,B) :-
not(on(A,B)),
A \== table,
A \== B,
clear_off(A), /* N.B. "action" used as precondition */
clear_off(B),
on(A,X),
retract(on(A,X)),
assert(on(A,B)),
assert(move(A,X,B)).
clear_off(table). /* Means there is room on table */
clear_off(A) :- /* Means already clear */
not(on(_X,A)).
clear_off(A) :-
A \== table,
on(X,A),
clear_off(X), /* N.B. recursion */
retract(on(X,A)),
assert(on(X,table)),
assert(move(X,A,table)).
A recursive action specification can have the form
action :- preconditions or actions,
retract(affected_old_properties),
assert(new_properties).
Assume again that the original situation holds (and that the previous 'move' clauses have been retracted):
on(a,b). on(b,c). on(c,table).
Now,
?- r_put_on(c,a). yes ?- listing(on), listing(move). on(a,table). on(b,table). on(c,a). move(a,b,table). move(b,c,table). move(c,table,a). yes
The 'put_on' action has recursively called the 'clear_off' action so that 'c' could be placed on top of 'a'.
Let us now add to the program some clauses so that a list of 'on' properties could be established jointly.
do(Glist) :-
valid(Glist),
do_all(Glist,Glist).
valid(_). /* Temporary. See Exercise 2.19.1 */
do_all([G|R],Allgoals) :- /* already true now */
call(G),
do_all(R,Allgoals),!. /* continue with rest of goals */
do_all([G|_],Allgoals) :- /* must do work to achieve */
achieve(G),
do_all(Allgoals,Allgoals). /* go back and check previous goals */
do_all([],_Allgoals). /* finished */
achieve(on(A,B)) :-
r_put_on(A,B).
The program can now be used by giving a main goal of the form ?- do([...]), where the list contains various on(-,-) subgoal statements (with no variables). Assume that the original starting situation holds again; that is,
on(a,b). on(b,c), on(c,table).
Consider the Prolog goal
?- do([on(a,table),on(b,a),on(c,b)]). yes ?- listing(on), listing(move). on(a,table). on(b,a). on(c,b). move(a,b,table). move(b,c,a). move(c,table,b). yes
The reader should try the goal and list the resulting program to partially verify that this works the way that we have claimed. This program does nothing special with the plan, other than incorporate it at the end of the program. To generate another plan for the same initial setup, but different goal conditions, one could reload plans.pro first. This inconvenience could be eliminated in several ways, depending on how one intended to use the program (see the exercises for more on this).
Pay particular attention to how the program attempts to satisfy a list of individual goals. The definition of the predicate 'do-all' in the program should be studied carefully. In satisfying a list of individual goals, each goal is worked on from left to right. If an individual goal is already satisfied, then proceed to the next goal. Otherwise satisfy the current goal, but then go back to the beginning of the list to check that the previous goals are still satisfied. Work on them again if they are not still satisfied. Repeatedly do this until all individual goals in the list are satisfied (if possible).
The STRIPS planning system, described in Nilsson (1980), used operators consisting of three components:
Precondition formula, which must be true in order for the operator to be applicable; Delete-list, which consists of predicates made false by the action; Add-list, which consists of predicates made true by the action.
The last 'clear_off' clause could be characterized in the STRIPS manner, as follows:
clear_off(A) : Precondition: A \== table, on(X,A), clear_off(X) Delete-list: on(X,A) Add-list: on(X,table), move(X,A,table)
Actually this would correspond to the recursive version of STRIPS (RSTRIPS) for the same reason that our program used recursive action specifications. The program presented here uses Prolog as the inference control engine, whereas STRIPS had its own inference and control strategies. A good project would be to read more about STRIPS, and re implement it in Prolog.
The Prolog planning program illustrates several other planning issues. An important thing to notice is that individual goals may not be independent of one another. For example, using the original starting configuration, suppose that we pose the goal
?- do([on(c,b),on(b,a),on(a,table)]).
which is the reverse of the previous goal. This time, the following plan is generated.
move(a,b,table). move(b,c,table). move(c,table,b). move(c,b,table). move(b,table,a). move(c,table,b).
Compare this plan with the one previously generated. This plan has redundant moves (like the middle two), and does not otherwise achieve the final conjunction of goals in as efficient a fashion as the plan for the first goal did. Note that the first attempt was more efficient because it sought to satisfy conditions first that represented "lower" blocks in the final finished plan, and then sought to satisfy conditions that represented "higher" blocks in the finished plan. This illustrates that individual goals in a conjunctive goal list may not be independent. In the planning literature this condition is called linearity; linearity means that the individual subgoals can be sequentially satisfied in any arbitrary order. Our example shows that linearity (or independence) is not always the case. In addition, some conjunctive goals are not even possible. For example,
?- do([on(a,b),on(b,a)].
represents a list of incompatible goals: not both goals can be true at once, under the assumptions that have been made. What will happen if one asks this goal?
Exercise 2.19.1 Formulate a concept regarding a valid list of goals, that is, whether all of the goals could be jointly true for actual physical blocks, and design a Prolog program to test whether a list of goals is valid. Remember that the original intention was not to allow blocks to overlap. Note that [on(a,b),on(b,a)] is logically consistent, but not valid.
Exercise 2.19.2 Eliminate assert and retract from the program by using appropriate extra parameters (representing state lists and action lists) in the definitions. Prolog purists might prefer this new version because it does not produce the side effects of assert and retract.
Exercise 2.19.3 Write a program that can detect and eliminate redundant steps in a plan.
Exercise 2.19.1 is especially interesting. Note that validity is supposed to capture the meaning of "physically possible". The use of the term valid differs from, but is directly related to, the term of the same name from logic. In logic "valid" means true in all possible interpretations. Here "valid" means true in all intended interpretations for the blocks world.
We would like to be able to make the following stipulations:
Soundness stipulation: If P0 is an initial program specifying a valid set of on-conditions, and if a1,a2,...,an is a sequence of actions, then the resulting program Pn is valid.
Completeness stipulation: If P0 is valid and if P is valid, then there is some sequence of actions a1,...,an and corresponding programs P1,...,Pn such that P1 results from action a1 performed on P0, P2 results from performing action a2 on P1, ..., Pn results from performing action an on Pn-1, and P=Pn.
A paraphrasing of the soundness stipulation states that if one starts with a valid set of on- conditions and performs a sequence of actions, then one winds up in a valid situation.
A paraphrasing of the completeness stipulation states that, given any valid first arrangement of blocks, and any valid second arrangement, there must be some sequence of actions that can be performed to bring about the second arrangement starting from the first arrangement.
Exercise 2.19.4 Using your formulation of validity, can you prove the soundedness and completeness stipulations?
It is possible to give a state-transition formulation to the action specifications. For example, we could consider the initial state to be the program P0=(..., on(a,b),on(b,c),on(c,table)) (written as a sequence) that we had previously specified. The action specifications and other clauses do not vary. Performing actions transforms one program into another. The transition function T can be expressed as
T : P x A --> P
where P refers to the program states and A refers to actions. The actions are the grounded heads of the action specification clauses. For example,
T(P0,r_put_on(b,a)) = P1
where P1=(...,on(a,table),on(b,a),on(c,table),...), or pictorially,
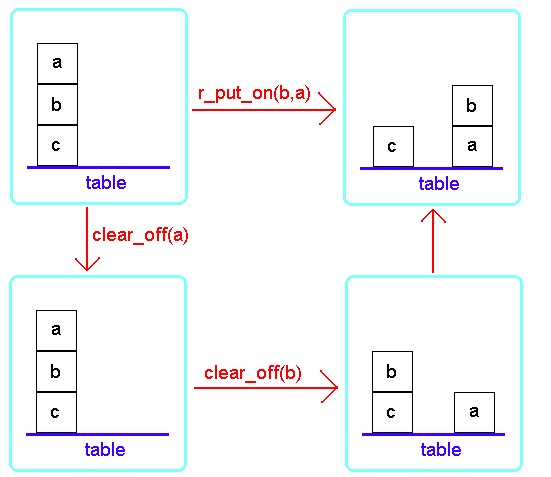
Exercise 2.19.5 Starting with the same P0 as used above, draw a diagram showing the transitions that can be used to transform P0 into P=(..., on(c,a),on(a,table),on(b,c),...). Identify the intermediate program states that are the results of single actions.
Exercise 2.19.6 For the mathematically inclined, formulate more careful definitions for P (the programs) and A (the actions).
Chapter 7 has more information regarding the use of Prolog to create executable specifications for system prototypes, using the action specification method.