2.15 Graph structures and paths

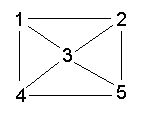
As an example, consider the following connected graph:

The edges can be represented in Prolog as facts:

edge(1,2).
edge(1,4).
edge(1,3).
edge(2,3).
edge(2,5).
edge(3,4).
edge(3,5).
edge(4,5).

To represent the fact that the edges are bi-directional we could either add eight more 'edge' clauses (edge(2,1),etc.) or we could try a rule like:

 (*)      edge(X,Y) :- edge(Y,X).

This is not a good idea, however. To see why it is not a good idea, try the following goal.

?- edge(5,1).

Notice that the rule (*) will be tried over and over in an infinite loop, so the goal will not terminate. Try it! A better way to handle this is to use a rule such as the following.

connected(X,Y) :- edge(X,Y) ; edge(Y,X).

Note the use of disjunction ';' in this rule. This rule could have been written as two rules:

connected(X,Y) :- edge(X,Y).
connected(X,Y) :- edge(Y,X).

We wish to develop a Prolog definition which generates paths between any two nodes of the graph. More specifically, we require the following (kind of) behavior for the predicate 'paths'.

?- path(1,5,P).
P = [1,2,5] ;
P = [1,2,3,5] ;
P = [1,2,3,4,5] ;
P = [1,4,5] ;
P = [1,4,3,5] ;
P = [1,4,3,2,5] ;
P = [1,3,5] ;
P = [1,3,4,5] ;
P = [1,3,2,5] ;
no

The paths are represented by the list of nodes through which one must travel to get from node 1 to node 5. Here is a definition for paths:

path(A,B,Path) :-
       travel(A,B,[A],Q), 
       reverse(Q,Path).

travel(A,B,P,[B|P]) :- 
       connected(A,B).
travel(A,B,Visited,Path) :-
       connected(A,C),           
       C \== B,
       \+member(C,Visited),
       travel(C,B,[C|Visited],Path).  

A declarative reading for the first clause amounts to "A path from A to B is obtained if A and B are connected". A declarative reading for the second clause amounts to "A path from A to B is obtained provided that A is connected to a node C different from B that is not on the previously visited part of the path, and one continues finding a path from C to B". Avoiding repeated nodes ensures that the program will not cycle endlessly.

Exercise 2.15 Suppose that edges have lengths. How does one calculate shortest paths between points in Prolog? Hint: One can use the setof goal, discussed in §2.12 and §4.15 ...

shortest(A,B,Path,Length) :-
   setof([P,L],path(A,B,P,L),Set),
   Set = [_|_], % fail if no path 
   minimal(Set,[Path,Length]).