Fig. 2.14
The following program simulates a parser/acceptor for an arbitrary deterministic finite automaton (DFA). When this and a state table program are loaded into Prolog, the parser/acceptor may be used to check inputs to the DFA to see whether or not they are acceptable. The program traces its action using write statements; these have been indented in order to better display the logical structure of the clauses.
parse(L) :- start(S),
trans(S,L).
trans(X,[A|B]) :-
delta(X,A,Y), /* X ---A---> Y */
write(X),
write(' '),
write([A|B]),
nl,
trans(Y,B).
trans(X,[]) :-
final(X),
write(X),
write(' '),
write([]), nl.
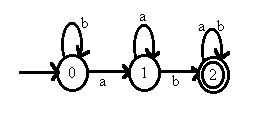
As an example, the following Prolog code specifies a state table for a DFA that accepts the language (a,b)*ab(a,b)* .
delta(0,a,1). delta(0,b,0). delta(1,a,1). delta(1,b,2). delta(2,a,2). delta(2,b,2). start(0). final(2).
A state diagram for this machine is as follows:

Suppose that both the driver program and the state table program are loaded ...
?- parse([b,b,a,a,b,a,b]). 0 [b,b,a,a,b,a,b] 0 [b,a,a,b,a,b] 0 [a,a,b,a,b] 1 [a,b,a,b] 1 [b,a,b] 2 [a,b] 2 [b] 2 [] yes ?- parse([b,b,a]). 0 [b,b,a] 0 [b,a] 0 [a] no
Exercise 2.14 Modify dfadrivr.pro so that it becomes a parser for NFAs, nondeterministic finite automata. Why is this extension such a natural one for Prolog?
Exercise 2.15 Using the DFA simulator presented here as motivation, design a Prolog simulator for Turing machines.