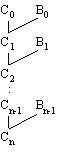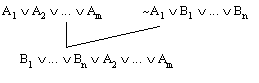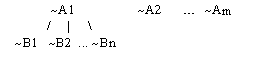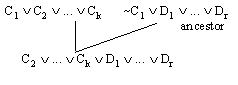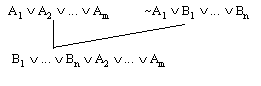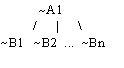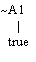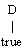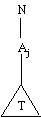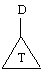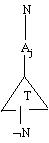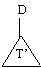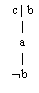
Theoretical Basis
for
Visual Logic
A Technical Report, draft #5
(11/16/95, last modified 6/20/96) © JRFisher
John R. Fisher
Computer Science Department
California State Polytechnic University
Pomona California
jrfisher@csupomona.edu
Abstract. Logic programs with classical negation are defined.
The analysis of these programs is based in a fundamental way upon the theory
of sets of disjunctive clauses, which was the basis of theorem-proving theory
in the 1960s and early 1970s. Like arbitrary sets of disjunctive clauses,
these logic programs can be classically inconsistent, or unsatisfiable.
Although such programs may be classically trivial (every proposition is
a theorem), this need not be the case for interesting subprograms. The paper
motivates and defines the concept of a supported proposition, using definitions
based upon clause trees. Supported propositions are supposed to be relatively
safe logical consequences of certain consistent subprograms. The paper provides
theorems showing relationships to classical satisfiability and logical
consequence, and provides references to algorithms that compute the concept
of supported propositions for finite logic programs with classical negation.
In addition, the paper discusses current work concerning the graphical
visualization of the various tree-based logical concepts, and a visual logic
system.
Clauses
A disjunctive clause has the form
L1 v L2 v ... v Ln
where the Li are literals, n >= 0. When n = 0, the clause is the empty
clause, referred to as nil. Positive literals are written in the
usual way, e.g., ‘p(X,a)’, and negative literals are written using ‘~’,
e.g., ‘~p(X,a)’. The negation of literal L is written as ~L. For
specific literals, double negations are absorbed, e.g., ‘~p(X,a)’ and ‘p(X,a)’
are classical negations, each of the other. This convention will be consistent
with a classical semantics for negation, which is what will be
used throughout the paper. If C = L1 v L2 v ... v
Ln and C' = L1' v L2' v ... v Ln' are two
disjunctive clauses such that C' results from C by renaming variables and
reordering of literals then C' is a variant of C; the relation
of being a variant is reflexive, symmetric and transitive.
A directed clause has the form
A1 | A2 | ... | Am < - B1 , B2 , ... , Bn
where m,n >= 0. This directed clause corresponds to the disjunctive
clause
A1 v A2 v ... v Am v ~B1 v
~B2 v ... v ~Bn
The directed clause is said to be positive if m>=1 and each
of A1, ..., Am, B1, ..., Bn is a positive literal. The directed clause
is said to be a definite clause provided m=1. Directed clauses
are used in program specifications (see following), possibly to emphasize
some specific relationships. However, the meaning of a program, or a subprogram,
will be determined (in so far as it can be determined using classical logic)
by the disjunctive clauses. If C and C’ are two directed clauses whose
corresponding disjunctive forms are variants (same except for variable renaming),
then C and C’ are also said to be variants of one another.
Logic Programs with Classical Negation
A logic program with classical negation is specified by giving a finite
collection of directed clauses of the form
A1 | A2 | ... | Am < - B1 , B2 , ... , Bn
where each Ai and Bj are literals, m > 0, n >= 0. One says that
C is a directed clause of P provided some variant of C occurs in
the specification of P. A subprogram of P is a subset of P. The program
P is positive provided some specification of P uses all positive
directed clauses. The program P is positive definite provided that
P can be specified using directed clauses which are both positive and definite.
Consider the following sample logic program with classical negation:
a(X) | b(X) < - c(X), d(X)
c(X) | a(X) < -
d(X) < - e(X)
e(1) < - e(2) < -
g(X,Y) < - a(X)
g(X,Y) < - b(Y)
~d(X) < - e(X), h(X)
h(2) < -
In this report, most of the subsequent technical definitions refer to
ground logic programs with classical negation. Using the constants in the
sample program, one would consider the following ground program:
a(1) | b(1) < - c(1), d(1)
a(2) | b(2) < - c(2), d(2)
c(1) | a(1) < - c(2) | a(2) < -
d(1) < - e(1) d(2) < - e(2)
e(1) < - e(2) < -
g(1,1) < - a(1) g(1,1) < - b(1)
g(1,2) < - a(1) g(1,2) < - b(2)
g(2,1) < - a(2) g(2,1) < - b(1)
g(2,2) < - a(2) g(2,2) < - b(2)
~d(1) < - e(1), h(1)
~d(2) < - e(2), h(2)
h(2) < -
Programs may have function symbols. But the assumption for the technical
definitions shall be that the logic programs with classical negation
are grounded, and have a finite number of clauses. It is possible
to greatly relax this restriction, but it is considerably easier to give
the basic definitions using this assumption. Ground literals will also
be called propositions.
An interpretation of a logic program with classical negation is an assignment
I of truth value (true or false) to the
ground literals and the clauses of the program in such a way that,
I(true) = true
for each literal L of P:
I(~L) = true if I(L) = false
I(~L) = false if I(L) = true
for each directed clause of P:
I(A1 | A2 | ... | Am < - B1, B2, ... , Bk) = false
if I(B1) = I(B2) = ... = I(Bk) = true
,
but I(A1)=I(A2) = ... = I(Am) = false
otherwise
I(A1 | A2 | ... | Am < - B1, B2, ... , Bk) = true
Note that such an interpretation assigns the same truth value to a directed
clause as a "classical" interpretation would assign to the corresponding
disjunctive clause. A logic program P with classical negation is said to
be consistent or satisfiable provided there is a interpretation
that gives every clause of P the value true. Such an
interpretation is a model for P. Otherwise, P is said to be inconsistent
or unsatisfiable. Note that a program is satisfiable if and only
if the set of disjunctive clause forms corresponding to the directed clauses
is satisfiable. The sample program is unsatisfiable, as will be evident
shortly.
If P is a logic program with classical negation, then a disjunctive
state for P has the form D = A1 | ... | An where n > 0, each Ai
is a literal (or the negation of a literal) appearing in P, and each constant
appearing in D appears somewhere in P. The "state" terminology comes from
[RLM]. For n=1, states are the same as literals.
An interpretation of a logic program with classical negation can be extended
to disjunctive states in the following "natural" way. Suppose that D =
A1 | ... | An is a state. Then, for interpretation I as previously defined,
I(D) = true provide I(Ai) = true for at
least one i. Otherwise I(D) = false. Thus, states are
interpreted as classical disjunctions. State D is a logical consequence
of program P provided that every interpretation making each clause of P
true must also assign true to D. (This
is vacuous, of course, if P is inconsistent.) When P is consistent and D
is a logical consequence of P, write P |= D.
Proposition 1. If P is a positive logic program, then P is consistent.
proof. The interpretation of P which assigns true
to each positive proposition (and false to the contraries)
is a model for P. �
Directed Clause Trees
{Note added 8/28/98: For a more formal mathematical treatment of the definition
of a clause (or rule) tree, see for example the subsection called "Rule Trees"
in the Positive Logic section (#2) of Logic Topics. The kind
of formal definition given there can be adapted to cover the definition given
here. }
Suppose that P is a logic program with classical negation, and that
D = A1 | ... | An is a nonempty disjunctive state for P. A directed
clause tree rooted at D is either D itself, or if
Ai | ... | Aj < - L1 , L2 , ... , Lk
is a directed clause of P, {i, ..., j} is a nonempty subset of {1, ...,
n}, and T1, T2, ... , Tk are clause trees rooted at literals L1 , L2 , ...
, Lk respectively, then the tree formed by root D with (unordered) child
trees T1, T2 ...,Tk is a directed clause tree rooted at D:
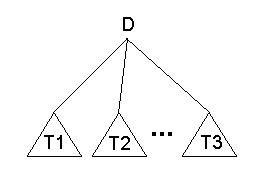
Fig. 1
As a special case, consider unit clauses like
c(1) | d(1) < - or ~a(1) < -
These clauses form simple trees
c(1) | d(1) ~a(1)
| |
| |
true true
That is, take ‘true’ to be a unit clause of every logic program with classical
negation, and take unit clauses to have either their short form (e.g.,
‘~a(1) < - ‘ ) or the expanded form (e.g., ‘~a(1) < -
true‘ ).
Some interesting trees for the sample program are
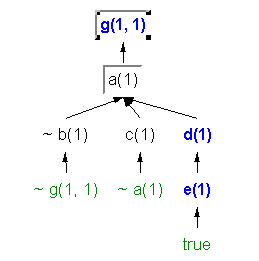
(a)
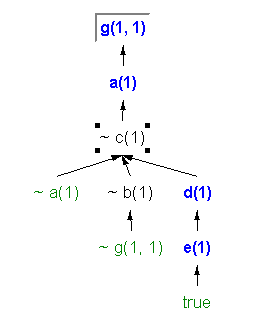
(b)
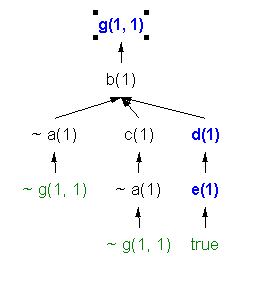
(c)
Figure 2
The directed clause trees of Figure 2 were drawn by a "visual logic" tool
that will be described later in this report. The reader should pause so
as to be sure to understand that variants of the directed clauses in the
original program specification have been used to construct the clause trees
-- NOT just the the clauses given in the original program specification.
Remember that a directed clause of the program is either a specified
clause or a variant of a specified clause.
The only node in a clause tree that could have more than one disjunct
is the root. Here is a clause tree having a disjunctive root
a(1) | b(1)
/ \
c(1) d(1)
| |
~a(1) e(1)
|
true
Figure 3
(The visual logic tool cannot display these kinds of trees at this writing.)
A closed clause tree rooted at state D is a clause tree T rooted
at D, as previously characterized, such that each leaf of T is either
- ‘true’, or
- of the form ~q where q is an ancestor of ~q in T, or if q is one
of the disjuncts in the root D of T.
Each clause tree displayed in Figures 2 and 3 is closed.
Suppose that S is a set of disjunctive clauses, and suppose that C0 belongs
S. A linear deduction of Cn from S with top clause C0 is a deduction of
the following form
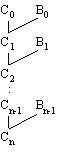
Figure 4
where each Ci+1 is a resolvent of Ci and Bi, for i = 1,...,n-1, and each
Bi is either a clause from S or Bi is Cj for some j < I. This definition
is taken from Chang and Lee [CL]. A linear refutation of C0 from S is a
linear a linear deduction of the empty clause from S with top clause C0.
Chapter 7 of [CL] proves that linear resolution is "refutation complete":
If C is a clause in an unsatisfiable set S of clauses and if S \
{C} is satisfiable, then there is a linear refutation of C from S.
Actually, this result is shown for OL-refutation using ordered clauses
and so-called framed literals.
The following algorithm converts a linear refutation of A1 v
A2 v ... v Am to a forest (set) of closed clause trees
rooted at ~A1 , ~A2 , ..., ~Am. An example follows the statement of the
algorithm.
For each resolution step in order, from the top down:
1. For the top clause in the linear refutation
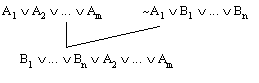 start the forest of clause trees thus:
start the forest of clause trees thus:
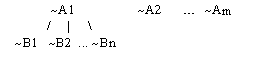
2. For a resolution step using an ancestor ...
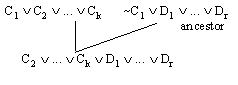
a. If C1 is not an ancestor of ~C1 in the forest, then erase
the node ~C1 in the forest.
b. If C1 is an ancestor ~C1 in the forest, then do nothing.
3. If the resolution step uses a side clause
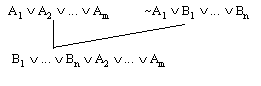 then replace every tree in the forest rooted at ~A1 by the tree
then replace every tree in the forest rooted at ~A1 by the tree
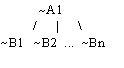 unless n=0, in which case replace every tree in the forest rooted at ~A1
by the tree
unless n=0, in which case replace every tree in the forest rooted at ~A1
by the tree
For example, the linear refutation on the left below is
converted to the forest of closed clause trees on the right. The ‘*’ in the
linear refutation refers to the ancestor ‘b’. Actually, the clause tree
started at the beginning with root ‘~b' is erased at the point where the
ancestor resolution is applied. Note, however that there is a closed clause
tree rooted at ‘~b' which occurs as a subtree of the tree rooted at ‘~a’.
(The dotted line in the diagram is used to illustrate this.) If one makes
allowance for this possibility -- that some of the closed clause trees
may wind up being subtrees of others -- then one has the proposition following
the figure.
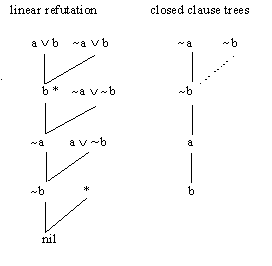
Figure 5
Note that explicit factoring is needed for linear resolution (e.g., the
first resolution on the left above). The clause tree approach has no need
of factoring.
Proposition 2. The conversion algorithm converts a linear refutation
of top clause A1 v A2 v ... v Am using side clauses
from S to a forest (set) of closed clause trees rooted at ~A1 , ~A2 , ...
, ~Am using directed versions of the clauses in S.
proof. The conversion algorithm clearly converts the resolution
refutation into a forest which has tree roots as claimed. Consider any leaf
L of any tree in that forest. If L is neither ‘true’ nor the negation of
one of its ancestors, in the same tree, then the last occurrence of ~L in
the linear refutation must have occasioned resolution against some side
clause in S. But in that case, the occurrence of L in the tree (in the forest)
should have branches growing from it and L would not be a leaf. Thus each
tree in the forest is closed. �
If T is a closed clause tree rooted at state D, then define
P(T) = {C | C is a ground clause of P used to construct T}
Proposition 3. If there is a closed directed clause tree T rooted
at D and P(T) is consistent, then P(T)|= D.
proof. Suppose that D = A1 | ... | Ak. First of all, consider
only cases where T has all ‘true’ leaves. Use induction on the height of
T, where the height of a tree that is only a root is 0, and the height of
other trees is 1 + max{height of subtrees}. The smallest height of a closed
clause tree is 1, and such a tree must have the form
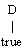
Figure 6
and it follows that P(T) |= D. Assume that the proposition is true for
all P where T has only ‘true’ leaves and the height of the tree is less than
h. Suppose that closed clause tree T does have height h. T has form
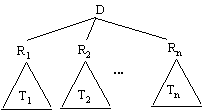
Figure 7
where Ri is root of Ti, 1=1,...,n. Note that
P(T) = {C} U {P(Ti) | i=1,...,n}
where C is the directed clause instrumental in forming the branching at
root D, and each P(Ti) is consistent. Since each Ti has height less than
h, P(Ti) |= Ri, and consequently, P(T) |= Ri, for each i=1,...,n. Thus,
each body literal of the directed clause C is a logical consequence of P(T),
and therefore the head of C is a logical consequence of P(T), and hence
P(T) |= D, as required.
Now consider the general case -- when the leaves of T are not necessarily
‘true’. This time use induction on the deepest contingent leaf. (For
now, a contingent leaf of a closed directed clause tree is any leaf which
is not ‘true’. This temporary definition will be consistent with the definition
of a contingent node given in the next section.) The base case is where
there are no contingent leaves (zero depth of deepest such). In this case,
each leaf is ‘true’, and this case has already been dealt with above. Assume
that the proposition holds for closed clause trees having deepest contingent
leaf at depth less than d, and suppose that T has deepest contingent leaf
at depth d > = 1. If D were not a logical consequence of PT, then
P(T) U { ~A1< -, ~A2< -, ... , ~Ak<
-}
would also be consistent. Modify T so that any leaf Ai is extended using
a branch to ‘true’
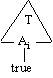
Figure 8
obtaining closed directed clause tree T’, also rooted at D. Now
P(T’) = P(T) U { ~A1< -, ~A2< -, ... , ~Ak<
-}.
Any node at depth one in T’ is rooted over a subtree whose deepest contingent
leaf has depth less than d. So T’ has the form
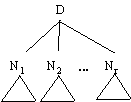
Figure 9
and by induction P(T’) |= Nj, j=1,...,r. In similar fashion to a previous
argument, T(P’) |= D. But P(T’) |= ~Ai, for i=1,...,k. So P(T’) could
not have been consistent, and thus it must be the case that D is a logical
consequence of P(T). �
An alternate proof of Proposition 3 could take the following approach:
a) Show that closed clause trees can be "converted" to linear refutations
using disjunctive clauses (a converse for proposition 2). b) Use the well
known result that linear resolution for disjunctive clauses is sound: S
consistent and S U {~C1 ,~C2 ,...,~Ck} inconsistent implies S |= C1 v C2
v ... v Ck. The details are not included here.
Proposition 4. If P is consistent and P |=D then there is a closed
clause rooted at D, constructed using directed clauses of P.
proof. Suppose that D = A1 | ... | Ak. Let N be a new proposition
not appearing in P, and let
P’ = P U {N < - A1, N < - A2, ... , N <
- Ak}
Now P’ is also satisfiable and P’ |= N. Thus there is a linear refutation
of P’ U {~N}, so by Proposition 1, there is a closed directed clause tree
rooted at N, which would have the form
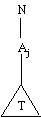
Figure 10
for some j, where T is a directed clause tree using directed clauses
from P’. If T does not have ~N as a leaf, then T is a closed directed clause
tree rooted at Aj and then
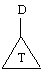
Figure 11
is a closed directed clause tree rooted at D. On the other hand, suppose
that ~N is a leaf of T.
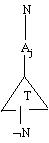
Figure 12
The parent node for ~N must be some ~Am. Erase N and ~N in the this
tree and replace Aj by D to obtain
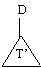
Figure 13
which is then a closed directed clause tree rooted at D. �
In the next section, an attempt is made to develop a reasonable converse
to proposition 4, in the following form: If D is supported using an
appropriate closed clause tree, then the subprogram used to construct the
tree is consistent, and D is a logical consequence of this subprogram.
Supported States
This section provides a technical definition of supported states, using
clause trees.
We say that state D is evident provided there is a closed clause
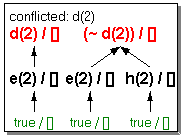
tree rooted at D. State D = A1 |...|An is said to be conflicted
provided D is evident and each ~Ai is also evident.
In the sample program, d(1), d(2), ~e(2), e(1), e(2), g(1,1), g(2,2),
~d(2), ~h(1), ~h(2), and h(2)are all evident propositions. So, for example,
d(2), e(2) and h(2) are conflicted propositions.
Proposition 5. If P is positive definite program then proposition
p of P is evident if, and only if, p belongs to the unique least Herbrand
model M(P) of P.
The least Herbrand model M(P) is the intersection of all (positive) Herbrand
models of P, as in [L].
A contingency annotated closed clause tree rooted at state D
is a closed clause tree T rooted at D, such that each node of T is annotated
with a set of contingencies, according to the following rules:
- each ‘true’ leaf is annotated with the empty set of contingencies
{},
- each leaf ~q is annotated with the set {q},
- if n is a branching node of T, having child nodes n1, n2, ...,
nk, with contingency sets C1, C2, ..., Ck, respectively, then the contingency
set annotating node n is the set
C1 U C2 U ... U Ck \ {the literals of n}
The last expression represents the union of the Ci with each literal of
n taken out. Note that only the root node of T would involve more than one
literal. The other nodes in T correspond to a single literal.
Proposition 6. Any closed clause tree can have contingency annotations
added to the tree.
A contingent node of a contingency annotated closed clause tree
T is any node of T annotated with a nonempty set of contingencies. A noncontingent
interior node is called a supporting node. If T is a contingency
annotated closed clause tree rooted at p, then define
C(T) = {n | n is a contingent node of T}
S(T) = {n | n is a supporting node of T}
Roughly, a contingent node in a contingency annotated closed clause tree
is a node that was involved in case-based reasoning. Such a node, in case
it is an interior node of the tree, is not necessarily a proposition to which
any particular commitment of truth value must be made.
A disjunctive state D of program P is said to be supported provided
that there is a closed clause tree rooted at D such that no interior node
of T is conflicted.
Proposition 7. If state D is supported, then D is evident.
Considering only the evident propositions previously mentioned, the reader
should carefully check to confirm that d(1), e(1), e(2), g(1,1), ~h(1),
h(2) are supported, according to the definition. There are no other supported
propositions. (But there are, of course, many other supported disjunctive
states.) For example, g(2,2) is not supported, as indicated by the following
trees ...
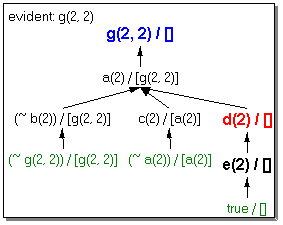
(a)
(b)
Figure 14
Actually, there are three closed clause trees demonstrating that g(2,2)
is evident, and Figure 14(a) is one of those trees. Each of those trees
uses node d(2), and d(2) is conflicted. Therefore, g(2,2) is not supported.
d(2)of the sample program is an example of what is technically defined
as a dilemma: A dilemma is a proposition p of P such that both
p and ~p are supported.
Proposition 8. Suppose that P is a logic program with classical
negation and suppose that D is supported using contingency annotated tree
T. Then each n in S(T) is supported, and ~n is not evident.
proof. The subtree T’ of T rooted at n is a contingency annotated
closed clause tree in its own right. ž
Proposition 9. Suppose that P is a logic program with classical
negation, and that D is supported using tree T. Then the supporting subprogram
P(T) is classically consistent, and D is a logical consequence of P(T).
proof. Suppose that P(T) is unsatisfiable. According to the
lemma below, there is some literal q of P(T) and satisfiable subsets P’
and P’’ of P(T) such that P’ U {q} and P’’ U {~q} are unsatisfiable. But
then, by Proposition 2, there would be a closed clause tree rooted at q,
constructed using clauses from P’, and a closed clause tree rooted at ~q
constructed using clauses from P’’, which would show that q must be conflicted,
contrary to the fact that the nodes of T are not conflicted, since p is
supported. (Note: one of q or ~q would necessarily be an interior node
of T.) Clearly, p is a logical consequence of the consistent set P(T).
ž
Lemma. Suppose that S is an unsatisfiable finite set of ground clauses.
Then there is some literal L appearing in S, and satisfiable subsets S'
and S'' of S such that S' U {L} and S'' U {~L} are unsatisfiable.
proof. The proof uses induction on the number of clauses in
S. The fewest number of clauses that S could have is two, and then S must
contain two unit literal clauses L and ~L, so that S' = {~L} and S'' =
{L} would satisfy the conclusion of the lemma. So assume that S has more
than two clauses and that the lemma is true for unsatisfiable sets of clauses
having fewer clauses than S.
Since S is unsatisfiable, there is some literal K such that K occurs
in a clause of S and ~K occurs in some (different) clause of S. Let S1 be
the set of all those clauses of S which do not have the literal K in them
and let S2 be the set of all those clauses of S which do not have the literal
~K in them. Both S1 and S2 are proper, nonempty subsets of S.
If either S1 or S2 is unsatisfiable, then, since each has fewer clauses
that S, the conclusion of the lemma would be true for the proper subset,
and hence true also for S.
Otherwise, both S1 and S2 are satisfiable. Then both S1 U {K} and S2
U {~K} must be unsatisfiable. [To see this, suppose that S1 U {K} were satisfiable,
having some model M. Then M would assign true to each
clause in the difference set S \ S1, since each clause in S \ S1 contains
the literal K. Hence M would satisfy S = S1 U (S \ S1), a contradiction,
since S is unsatisfiable. Similarly for S2 U {~K}.] Now the lemma follows
with L = K, S' = S1, and S'' = S2. ž
Corollary. The lemma is true for an arbitrary (not necessarily finite)
unsatisfiable set of clauses.
proof. If S is an arbitrary unsatisfiable set of ground clauses,
then some finite subset S1 of S is also unsatisfiable. The lemma applies
to S1 and gives the same conclusions in relation to S. ž
Pertinent States
Disjunctive state D = A1 |...| An is said to be pertinent provided
there is a state D1 = B1 |...| Bk such that D|D1 is evident but D1 is not
evident.
For example, for the program
a | b < -
c < - a
~c < -
D=c is pertinent since c|b is evident, as shown using the following closed
clause tree:
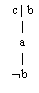
Figure 15
and D1=b is not evident.
A proposition p is potentially-conflicted provided both p and
~p are pertinent.
A disjunctive state D is strongly-supported provided there is
a closed clause tree T rooted at D such that each interior node of T is
not potentially-conflicted.
Proposition 8. The concepts 'pertinent', 'evident', 'strongly-supported',
and 'supported' are related as in the following diagram (arrows indicate
logical implication).
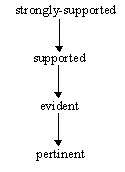
Figure 16
The definition of 'pertinent' resembles (but is different from) a definition
of a conclusion based on the generalized closed world assumption of [M].
Metalogic programs
Suppose that P is a logic program with classical negation. Roughly speaking,
a P-metalogic program is a logic program that specifies definitions
about P, based upon concepts, such as 'evident', 'supported', etc., defined
in previous sections. For example, given P in advance, the following program
specifies definitions of additional concepts:
believable (D) < --
supported(D),
classical_negation(D,N),
not supported(N).
knowable (D) < --
supported(D),
classical_negation(D,N),
not evident(N).
certain (D) < --
strongly-supported(D),
classical_negation(D,N),
not pertinent(N).
(A formulation that explicitly refers to the base program P could use
some notation like 'supported (D,P)', 'believable(D,P)', etc. ) The three
rules given above define three "levels of certainty" about D, based on support
for D and evidence for ~D. The terminology (e.g., "believable") is suggestive
but only used here as a technical term for the predicate. There is a large
hierarchy of possible situations; for example, another would be D evident,
~D not evident, and so on.
A metalogic program is a logic program whose clauses have the form
A < -- B1, ..., Bn, not C1, ..., not Cm
where A, each Bi, and each Cj is a positive literal, and each Cj must
be a positive literal whose predicate is one of the reserved predicates
'pertinent', 'evident', 'supported', 'strongly- supported' (or possibly
others). The displayed clause is considered as (part of) a definition of
its head literal A. (There could presumably be more than one clause defining
A).
Predicates in metalogic programs refer to properties defined for logic
programs with classical negation. Interpretations of such metalogic programs
must use the intended meanings for the reserved predicates, use the closed-world-assumption
for 'not' (since circularity has been avoided), and the obvious meaning
for 'classical_negation' (as per the conventions at the beginning of this
paper). Additional motivation for metalogic programs and the relevant details
will be presented elsewhere.
Computing the Concepts
Several approaches to computing the concepts of this paper can be taken.
Various Prolog programs are available from the author [F]. Several involve
complicated algorithms; and the finiteness assumption for programs is crucial
to the guaranteed termination of the algorithms. The next section discusses
an interesting graphical approach to computational logic.
Visual Logic
In the reference [T], Luu Tran describes a graphical software system
for visualizing and animating the tree-based logical concepts discussed
in this paper. That work has three main aims:
- To propose requirements for visual logic systems, and to relate these
concepts to visual programming, and multimedia programming,
- To implement tree-based logic visualizers in accordance with the
requirements specified in 1),
- To experiment with the implementations in 2) and make judgements
about the effectiveness of the graphical methods.
Various figures in this document (see Figures 2 and 14) have already illustrated
the appearance of some of the visual logic system tools. Using the system,
trees can be expanded incrementally ("rulewise"), or in a semiautomatic
fashion. Different techniques are explored for animating alternative derivations.
The visual logic system also explores the graphical input of logical information
by drawing trees.
Many of the goals and methods of visual logic overlap with goals and
methods used by graphical Prolog debuggers, such as those in [DC] and [EB].
The visual logic system is implemented using SWI-Prolog and XPCE [XPCE].
References
[CL] Chang, C., and Lee, R. C., Symbolic Logic and Mechanical Theorem
Proving, Academic Press, 1973.
[DC] Dewar, A.D. and Cleary, J.G., Graphical display of complex information
within a Prolog debugger, International Journal of Man Machine Studies,
25 pp. 503-521, 1986.
[EB] Eisenstadt, M. and Brayshaw, M., Graphical debugging with the Transparent
Prolog Machine (TPM), Proc. 10th International Joint Conf. on Artificial
Intelligence (IJCAI-87), 1987.
[F] Fisher, J.R., A Brief Introduction
to Visual Logic
[FT] Fisher, J.R., and Tran L., A Visual Logic, Proc. 1996 ACM Symposium
on Applied Computing (SAC'96), Philadelphia, Penn., pp. 17-21.
[L] Lloyd, J.W., Foundations of Logic Programming, Springer-Verlag,
1987.
[M] Minker, J., On indefinite databases and the close world assumption,
in Lecture Notes in Computer Science 138, pp. 292-308, Springer-Verlag,
1982.
[RLM] Rajasekar, A., Lobo, J., and Minker, J., Weak generalized closed
world assumption, J. Automated Reasoning, 5(3), 1989, 293-307
[T] Tran, L., Visual
Logic, Masters Degree Thesis, California State Polytechnic University,
Pomona, 1996.
[XPCE] http://www.xpce.nl.