Design and implementation

From the start, VL was not intended to be a fully functional, practical tool. Instead, the emphasis all along was on rapid prototyping and exploration with an eye on proposing specifications for a complete system. As such, the production process did not follow the design-implement-test-debug cycle but involved quite a bit of experimentation and trial-and-error -- perhaps too much trial-and-error which resulted in delaying the completion of the project.

VL was implemented entirely in SWI-Prolog and the add-on graphical package XPCE. The choice of Prolog has advantages as well as drawbacks. On one hand, the construction of clause trees is more or less an extension of Prolog’s inference engine and therefore can be elegantly captured with a few Prolog rules. In addition, Prolog is well-suited for rapid prototyping. On the other hand, the use of Prolog imposes some limitations and difficulties of its own. This section discusses some pertinent issues in the design and implementation of VL.

Dealing with disjunctive clauses

Though not stated in chapter 3, [Fisher96] allows logic programs with disjunction in the head and defines 'supported', etc. in terms of states (disjunctions of terms) rather than just single terms. For the sake of simplicity, VL does not handle disjunctive clauses directly (although this was a possibility raised in the thesis proposal). Instead, it converts clauses to equivalent contrapositive sets of clauses. That is, each clause of the form:

p₁ | p₂ | ... | p_n <- q₁, q₂, ... , q_m . n > 0, m > 0.

is converted to two sets of clauses:

p₁ :- ~p₂,~p₃, ... ,~p_n-1,~p_n, ..., q₁, q₂,... , q_m .
p₂ :- ~p₁,~p₃, ... ,~p_n-1,~p_n, ..., q₁, q₂,... , q_m .
...
p_n-1 :- ~p₂,~p₃, ... ,~p_n-2,~p_n, ..., q₁, q₂,... , q_m .
p_n :- ~p₂,~p₃, ... ,~p_n-2,~p_n-1, ..., q₁, q₂,... , q_m .

and

~q₁ :- ~p₁,~p₂, ... ,~p_n, q₂, q₃, ..., q_m-1, q_m .
~q₂ :- ~p₁,~p₂, ... ,~p_n, q₁, q₃, ..., q_m-1, q_m .
...
~q_m-1 :- ~p₁,~p₂, ... ,~p_n, q₁, q₂, ..., q_m-2, q_m .
~q_m :- ~p₁,~p₂, ... ,~p_n, q₁, q₂, ..., q_m-2, q_m-1 .

or, more succinctly:

p_i :- ~p₁, ... ,~p_i-1,~p_i+1,..., ~p_n, q₁, q₂,... , q_m . i = 1..n

and

~q_j :- ~p₁,~p₂, ... ,~p_n, q₁, q₂, ..., q_j-1,q_j+1 , ... , q_m . j =1..m

The first formula yields n clauses and the second yields m clauses. Hence, the conversion produces a total of n+m clauses.

For example, given the following set of clauses:

a | ~b | c <- d, ~e.
 d <- ~f.
~e <- true.

The above conversion produces:

 a :- b, ~c, d, ~e.
~b :- ~a, ~c, d, ~e.
 c :- ~a, b, d, ~e.
~d :- ~a, b, ~c, ~e.
 e :- ~a, b, ~c, d.
 d :- ~f.
~f :- ~d.
~e :- true.

For the last clause, ~e <- true. is equivalent to ~e <- . Since m=0, no conversion is needed. Note that even when the head of the clause is a single term (n=1), it is still necessary to convert the clause to its contrapositives in order to ensure that all inferences that could be made with the original set of clauses can be made with the resulting sets of contrapositives. To see why this is so, consider the following example:

Original clauses: 1) a|b<-true. 2) c<-a. 3) c<-b.

Contrapositives: 1) a:-~b. b:-~a. 2) c:-a. ~a:-~c. 3) c:-b. ~b:-~c.

Without at least one of the contrapositives { ~c:-~a,c:-~b }, it is not possible to show that c is evident via



Fisher calls such contrapositives back-links since they are used to "link back" to an ancestor [Fisher96]. Since according to classical logic each contrapositive clause is equivalent to the original clause, the conversion must be sound. However, a major problem with the conversion is that it leads to a large number of unnecessary clauses, that is, those which never lead to any useful derivation. Conceivably, a practical algorithm which performs some type of graph traversal can be devised to determine beforehand which back-links will be needed. The algorithm of course would have to employ some heuristics to avoid doing the work of inference engine itself! (As a trivial case, observe that if there are no clauses with disjunction in the head, then no back-links are necessary.) Since efficiency consideration was not a high priority, however, the current implementation of VL simply performs the conversion in full.

As an exception, VL adds any clause with a :- implication operator to the clause database as is. This allows for suppression of VL's automatic conversion of clauses to contrapositive forms at the programmer's discretion -- for example, in those cases when it is known beforehand that back-links are not needed -- thereby alleviating the redundancy problem. The other intended use for the :- notation is to denote utility relations (e.g., member/2) for which contrapositive conversion does not make sense or may lead to undesirable results.

Unification

Both Query mode and Explore mode rely on the Prolog interpreter to perform unification and therefore suffer anomalies due to lack of an occur check. However, this seems to be a reasonable tradeoff since a robust unification routine running on top of Prolog would have been unacceptably slow.

Loop detection

VL does not have a sophisticated loop detection scheme. Instead, it merely checks whether a node P is a 'repeat' of some ancestral node Q. In VL, P is said to be a 'repeat' node of Q if
• P and Q are structurally equivalent, or
• Q subsumes P, that is, Q is at least 'as general as' P.

P and Q are structurally equivalent if

• P and Q are both uninstantiated variables, or
• P and Q are equivalent atoms, or
• P and Q are structures with the same functor, arity, and structurally equivalent arguments.

Finally, Q subsumes P if, once all variables in P are bound with arbitrary atoms not occuring in Q, P and Q still unify.

For programs with no function symbols or programs which are completely grounded, the above test is guaranteed to detect infinte looping. For general programs with function symbols and non-ground terms, the test traps many but not all instances of infinite looping. Here is one example which fails: foo(X,1) :- ... , foo(1,X), ... . The subject of logic programs and loop detection is a difficult one in general. If at some later date, it is determined that VL should have a more rigorous method of infinite looping detection, see [Bol91] for an intensive work on this subject. Also, [Jones93] presents an algorithm for ensuring that a recursive literal in the definition of a predicate does not cause infinite recursion.

Query mode

The inference engine for Query mode builds on John Fisher's original program conflict.pro which finds conflicts in logic clauses. conflict.pro has been modified so that it 1) returns (in symbolic form) the contingency annotated clause tree along with the result and 2) is non-deterministic, i.e., capable of generating alternative solutions upon backtracking. The remainder of Query mode is the graphical interface that visualizes the calculated symbolic trees and interacts with the user.

Query mode only shows closed clause trees. In other words, it lists on the left pane only terms that are at least evident. Also, when Query mode displays a clause tree, it calculates all possible values (evident/supported/conflicted) for each node and colors the node according to the most 'general' value. For example, a node colored purple is supported but not moot. A distinction is made between global and local values. A node's global value refers to its overall calculated value which is not necessarily borne out by the tree it is in, whereas its local value always pertains the containing tree. Hence, in a given tree, a locally evident node must have an empty contingency set, whereas a globally evident node may or may not. (If the latter case, then there must of course exist some other tree in which the globally evident node does have an empty contigency set.) By default, Query shows global values for nodes. However, the user has the option of switching between showing global and local values.

Explore mode

Unlike Query mode, Explore mode does not pre-compute clause trees and node values. Instead, tree nodes are constructed, modified, and destroyed in real time in response to user commands. Individual node values are continually verified and updated as changes are made to the tree. For example, when the user expands node P, Explore performs (roughly) the following:
• Find a clause which matches P and which has not previously been used to expand P.
• Create a new child node for each of the terms in the clause body and attach the new node to P.
• Create the appropriate variable binding and propagate the binding to other nodes throughout the tree.
• Determine the value of each of the child node - 'true', 'ancestry resolved', 'repeat', 'blocked', or 'na' (none of these). Verify the values of the ancestor nodes - 'evident' or 'na' - according to the values of the new child nodes. Note that an ancestor node is possibly evident only when a new child node is either 'true' or 'ancestry resolved.'

The implementation exploits XPCE's object-oriented paradigm. Conveniently, XPCE has built-in classes for hierarchical trees and nodes and provides standard methods for handling them such as iterating through the nodes of a tree, adding children to an existing node, and displaying the tree in horizontal or vertical layout. Each node in the explore tree is an extension of the generic node class and has attributes and methods that govern its appearance and behavior. In addition, each node object is associated with records that encapsulate all the information pertaining to it. This information includes the node's state, value, current term, used clauses, and variable bindings. To a large extent, operations in Explore mode are performed by sending messages to and among nodes. For example, when a leaf node determines it is 'true' or 'ancestry resolved', it sends a message to its ancestor nodes telling each to verify whether it is evident (at the root of a closed clause tree). The implementation seems to point toward the interesting possibility of applying objected-oriented paradigm to logic and inference, although the thesis will not pursue the details of this side issue.

VL represents the user's program clauses and terms simply as Prolog terms and treats them as data. As mentioned previously, Explore mode uses Prolog to perform head clause matching and unification. On the other hand, Explore must keep track of used clauses and variable bindings through each stage of tree expansion in order to uninstantiate variables and perform backtracking ('redo' in VL's terminology). The implementation details of maintaining variable bindings, performing variable propagation and uninstantiation, etc., are rather too complicated to delve into here. Instead, another difficult issue will be discussed next.

Defining a workable model for showing alternative derivations

Since Explore mode allows the user to expand and 'redo' (re-expand using a different matching clause), a problem that arises is how to ensure that all possible derivations can be obtained. In Prolog, the depth-first, left-most search makes it possible to impose a strict, unambiguous backtracking model that guarantees finding of all derivations. This is not the case with VL's Explore mode. Consider, for example, this simple program:

1) a( X, Y):- b( X), c( Y).
2) b( foo).
3) b( bar).
4) c( cat).
5) c( dog).

For the goal a(X,Y), the user should be able to get closed clause trees for {a(foo,cat), a(foo,dog), a(bar,cat), a(bar,dog)} in some order. Suppose the user expands the tree in depth first fashion as shown below (the number on the left indicates the order of node expansion; the set on the right indicates used matching clauses):



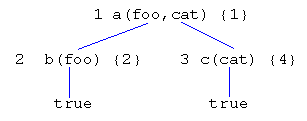
Next, suppose the user redoes node c(). (By default, the next unused clause -- c(dog) in this case -- will be used.) The tree then becomes:



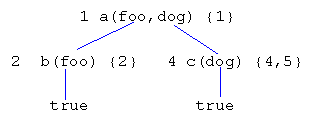
Node c()is now 'exhausted' (both matching clauses have been used). Next, the user redoes node b(). What should be done with node c() at this point? Arguably, it should be left alone since its term is not affected. The tree is now:



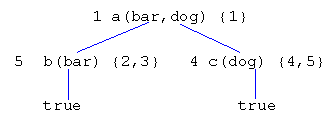
Now all nodes are exhausted, but one derivation, namely a(bar,cat), was missed. Obviously, the user needs to be able to somehow 'reuse', as it were, the matching clauses {4,5} for c(). One possible solution is to allow the user to manually select arbitrary matching clause when expanding / redoing nodes. Some mechanism can be employed to display all available clauses for a given node and to indicate which clauses have been used. The user then has the option of using a new or used clause. A serious drawback of this approach is that it places on the user the onus of having to keep track of the different combinations of used/unused clauses in order to extract all solutions. Clearly, this is not feasible with any but the smallest trees.

Next, consider a different approach. Suppose when node b() is redone in the final step, node c() is 'restored'. In VL's terminology, 'restoring' a node entails 1) resetting its term to the value to the point prior to the initial node expansion; and 2) resetting its set of used clauses to empty. This leads to the tree below. The user can now expand and redo c() to get a(bar,cat) and a(bar,dog) as desired.



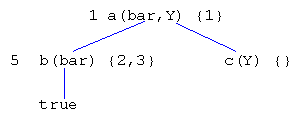
Again, the possibility of leaving it up to the user to manually perform 'restore' was considered and rejected as being too cumbersome. Instead, when a node P is redone, Explore mode automatically restores any node in the tree which was initially expanded after P. ('Initially expanded' refers to either the first instance the node is expanded or the first instance it is expanded after having been restored.) Note that Explore mode does have options for manually selecting a matching clause during expand/redo as well as manually restoring a node. However, the options are provided to give the user additional flexibility; they are not relied upon as a mean for obtaining all derivations.

In any event, the automatic restore feature is only part of the solution. Returning to the previous example, suppose the user expands then redoes node b() without ever expanding node c(). The (non-closed) clause trees obtained thus far are:



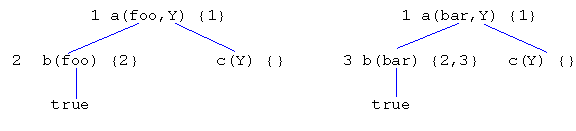
Subsequently, expanding and redoing c() only give closed clause trees for a(bar,cat) and a(bar,dog). b() will not be restored since it was initially expanded before c(). The problem in this case is that the tree was not completely expanded before the first redo. In fact, it can be shown through more complicated examples that in order to guarantee that all possible closed clause trees are obtained in Explore mode, the following rules must be observed:

• No nodes are left unexpanded when performing a redo.
• Nodes must be redone in the reverse order by which they were expanded, that is, always redo the node that was last expanded.

Explore mode provides a way for expanding and redoing nodes specifically designed to accommodate the above rules. The user can ensure that there are no unexpanded nodes before doing a redo with the 'Expand tree from root' command ('0' key). Likewise, using the 'Redo last' command ensures that the last node expanded is the first redone. Incidentally, the user can emulate Prolog's execution model by using only these two commands to expand and redo nodes.

Finally, a couple of points should be kept in mind. First, VL provides an easier and faster way of getting all derivations via Query mode. Therefore, being able to do the same in Explore mode is perhaps more important for the sake of completeness and less so from the point of practicality. Second, 'Explore' would seem to imply that the user is less interested in finding all derivations than in investigating pertinent parts of the tree -- a task Explore mode is better suited for