Discussion

Syntax

VL accepts as input text files consisting of clauses of the form:

p₁ | p₂ | ... | p_n <- q₁, q₂, ... , q_m . n > 0, m > 0.

or p :- q₁, q₂, ..., q_n . n > 0.

where vertical bars ( | ) represent disjunction and commas represent conjunction. Negation of a term is indicated by preceding it with a tilde ( ~ ). Otherwise, syntax for terms adheres to Prolog rules. That is, names and functors start with a lower case letter while variables start with an upper case letter. The underscore ( _ ) should be used in place of anonymous variables. Each clause must be terminated by a period. Note that disjunction is allowed only in the head. Clauses whose implication operator is :- are added to the clause database unchanged. Clauses whose implication operator is <- are converted to equivalent sets of all possible contrapositive clauses, as explained later.

"Semantics"

Since VL is intended to illuminate logical conflict, it is often used to investigate inconsistent programs. According to classical logic, inconsistent programs have no (classical) semantics. Therefore, it really does not make sense to talk about "semantics" in relation to the programs or clause sets that one studies with the aid of VL, except for some restricted instances. For example, given a consistent program, then the semantics for 'evident' is analogous to the semantics for 'satisfiability' in classical logic. On the other hand, a program such as

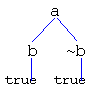
a <- b, ~b.
b <-.
~b <-

which is clearly inconsistent, has no classical semantics. The 'meaning' of, say, evident(a) is derived solely from its formal definition, i.e., the ability to construct a closed clause tree



For a given program S and some supported proposition p, the clauses used to construct some closed clause tree T for p do form a consistent subprogram S_T such that S_T |= p (see Theorem 3). Nevertheless, S as a whole may be inconsistent and consequently has no classical semantics.

Hence, any mention of "semantics" in relation to VL and conflict theory must be done with care. In fact, [Fisher95] eschews using the term "semantics" altogether to avoid potential confusion. The preceding discussion is not intended to define a semantics for programs in VL, that is, for logical programs with classical negation. Rather, the purpose is to clarify matters by explicitly stating that there is in fact no semantics for such programs except in the narrowed sense discussed above. However, more work does need to be done regarding the semantics of the concepts underlying VL itself (as opposed to the programs studied with VL).

System predicates

For practical purposes, VL recognizes the special system predicate is/2 for numeric calculation. (Arithmetic capabilities can be used, for example, to propagate certainty values in expert system rules.) Any term X is Y is considered a 'true' node if and only if a) Y is a valid arithmetic expression and has no non-ground term and b) X unifies to the evaluation of Y; otherwise, the term is a blocked node (failure). In Explore mode, an is node typically remains blocked until the expression Y becomes ground, at which point Y is evaluated and the result unified with X. If both the evaluation and unification succeed, the node becomes 'true'; otherwise, it remains blocked.

In addition, VL recognizes the usual relational operators ( >, <, >=, =<, ==). Relational expressions are handled similarly to arithmetic expressions.