Clause trees and linear resolution

Let S be a set of disjunctive clauses and C ∈ S, a linear deduction of C_n from S with top clause C_o is a deduction of the form



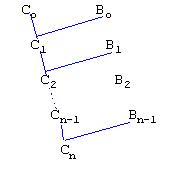
where each C_i+1 is a resolvent of C_i and B_i, 0 <= i <= n-1, and each B_i is either in S or a previous resolvent C_j, j<i. A linear refutation of C_o from S is a linear deduction of the empty clause from top clause C_o. [Chang73] shows that if S is unsatisfiable but S \ {C} is satisfiable, where C is a clause in S, then there is a linear refutation of C from S.

Clause trees and linear refutation are closely connected. Let S be a set of disjunctive clauses and S' be its corresponding set of directed clauses. [Fisher96] shows that any linear refutation of C = p₁ v p₂ v ... p_n from S can be converted to a set of closed clause trees T₁, T₂, ..., T_n rooted at ~p₁, ~p₂, ... ~p_n respectively, where each T_i is constructed using clauses from S'. Conversely, any closed clause tree rooted at p and constructed using clauses from S' can be converted to a linear refutation of ~p from S.

For example, the set of disjunctive clauses corresponding to the sample logic program is S = { a v ~b v c v ~d, ~a, b, ~b v ~e v ~f, ~c v b, ~c, d v a, d v ~e, e v ~c, e v ~a v ~f, f }. Below are the clause tree rooted at a and the corresponding linear refutation of a from S.



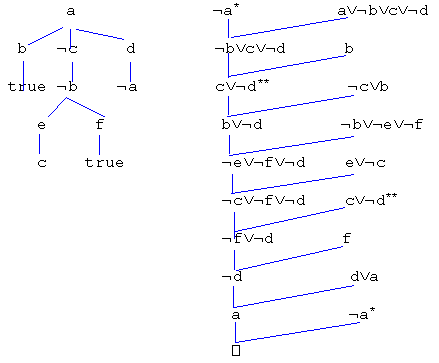
Hence, well-known results for linear resolution may be applied to clause trees. Linear resolution is important in part because it is relatively efficient and can be easily implemented on a computer. Clause trees, on the other hand, have the advantage of being more compact and readable.