Definitions

Evident, conflicted, and supported propositions

Let S be a logic program with classical negations and p be a term in S.

• If there is a closed clause tree T rooted at p, then p is said to be evident.

• If both p and its negation ~p are evident, then p is said to be conflicted.

• If there is a closed clause tree T rooted at p such that none of the interior nodes in T is conflicted, then p is said to be supported. By definition, if p is supported, then p is evident.

An example

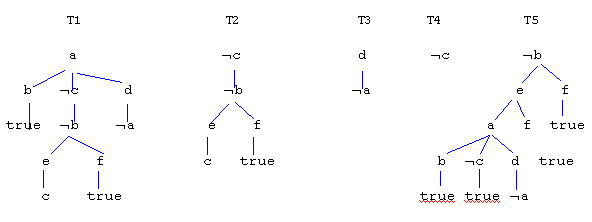
a <- b, ~c, d.        ~a <-      
b <-                  ~b <- e, f.    ~c <- ~b.      ~c <-         
d <- ~a.              d <-  e.          
e <-  c.              e <-  a, f.    f <-



Five sample clause trees are shown here. Note that only T1, T2, and T5 are closed.. Only a, ~a, b, ~b, ~c, d, e, and f are evident. a, ~a, b, and ~b are conflicted. Only ~a, b, ~c, and f are supported. As a clarification, consider ~c. There is a closed clause tree rooted at ~c (T2); therefore ~c is evident. Its negation, c, is not evident since a closed clause tree rooted at c cannot be constructed. Looking at T2, it would seem ~c is not supported since one of its interior nodes, ~b, is conflicted (b is trivially evident and ~b is evident as shown by T5). However, another closed clause tree for ~c, namely (~c --- true), shows that it is.

Whether the above definition of 'evident' and 'support' agree with an intuitive or pedantic understanding of these concepts is debatable, and indeed no claim is made to that effect. We simply note that it is useful to define and talk about 'evident' and 'supported' in the manner described here without asserting, for instance, that this is in fact what people really mean when they use these terms.

Returning to tree T1 in the example, note that the subtree rooted at c is itself a closed clause tree. In contrast, the subtree rooted at, say, b is not a closed clause tree. Hence, there is a difference between c and b which can be made explicit through the notion of a contingency annotated closed clause tree.

Contingency annotation

A contingency annotated closed clause tree T rooted at p is a closed clause tree rooted at p in which each node in T is annotated with a set of contingencies as follows:
• each 'true' leaf is annotated with the empty set {}.
• each non-true leaf is annotated with a set containing solely of its negation.
• each non-leaf node is annotated with the union of its children's contingency sets minus itself; i.e., if node n has children nodes n₁, n₂, ..., n_k whose contingency sets are C₁, C₂, ..., C_k respectively, then n is annotated with the set C₁, C₂, ... C_k \ {n}.

Here is T1 with contingency set annotation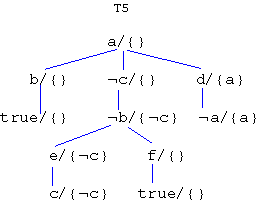

In a contingency annotated closed clause tree, any node with a non-empty contingency set is called a contingent node. An interior node with an empty contingency set is called a supporting node. In T5, b is a contingent node while c is a supporting node. Roughly speaking, a contingent node is a node that was involved in case-based reasoning. It is not necessary to commit to any truth value concerning a contingent node [Fisher96]. In T5, for example, b is neither evident nor supported but is used 'in a contingent manner' to support c. A supporting node, on the other hand, is a stronger assertion since it is itself evident and possibly supported.