Proposal for a full system

VL is fairly functional prototype which requires many small enhancements and several major additions in order to become a full, practical system. Many of VL's shortcomings have already been discussed. This section examines these and other problems and proposes possible remedies for them.

Handling states and extended definitions

As mentioned earlier, [Fisher96] allows closed clause trees to have disjunctions of terms, or states, at the root (rather than just single terms). Likewise, definitions for 'evident', 'supported', and 'conflicted' are applied to states. Hence, VL should accept states in query, e.g. 'a(X)|b(Y)|c(X,Y)'. The implementation would require fairly straight-forward modifications to the current code. (See Appendix A for a quick-and-dirty Prolog program which computes 'evident' for states.)

Next, consider the following extended definitions given in [Fisher95]

Definition 4: Disjunctive state D = p₁ | p₂ | ... | p_n is said to be pertinent provided that there exists some D' = q₁ | q₂ | ... | q_m such that D|D' is evident but D' is not evident.

Definition 5: Proposition p is said to be potentially-conflicted provided that both p and p are pertinent.

Definition 6: Disjunctive state D is said to be strongly-supported provided that there exists a closed clause tree T rooted at D and none of the interior nodes in T is potentially-conflicted.

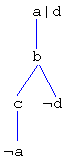
For example, given

a	<-  b.
b|d	<- c.
c	<-  ~a.

then a is pertinent since a|d is evident by



but d is not evident.

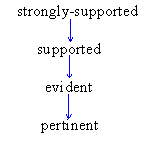
The hierarchical relationships among 'strongly-supported', 'supported', 'evident', and 'pertinent' are shown below. Note that 'evident' implies 'pertinent'.



Computing 'strongly-supported' and 'potentially-conflicted' is straight-forward once 'pertinent' is known. The interesting problem is how to compute 'pertinent' for a given state D. A brute-force approach would be to construct an arbitrary state D' from all possible combinations of literals appearing in the program (but not in D), verify that D' is not evident, and check whether D|D' is evident. Obviously, this is not feasible for all but the simplest programs. Here is (possibly) a more intelligent approach to constructing D':

1. Construct a set T of clause trees (not necessarily closed) rooted at state D in the usual way (see [Fisher96]). Annotate the nodes in each tree in T as follows:

   • each 'true' leaf is annotated with the empty set {}.
   • each ancestry-resolved leaf p is annotated with a set consisting solely of its negation {p}.
   • each 'blocked' leaf p which is not ancestry-resolved but which has no matching clause is also annotated with the set {p}.
   • each non-leaf node n = p₁ | p₂ | … | p_j (j1 for the root node, j=1 otherwise) with children nodes n₁, n₂, …, n_k is annotated with the set c₁ c₂ … c_k \ {p₁, p₂, … , p_j}, where c₁, c₂, …, c_k are the annotation sets for n₁, n₂, …, n_k, respectively.

     Except for the third condition, the annotation above is identical to the annotation for contingency sets.

2. If there exists some tree in T whose annotation set is {}, then D must be evident. By definition, it is also pertinent.

3. Otherwise, for some tree in T with a non-empty annotation set C = {p₁, p₂, … , p_j}, j1, let D' = p₁ | p₂ | … | p_j. If D' is not evident, then D is pertinent. (D|D' must be evident since D' absorbs the C, leaving an empty contingency set.)

From the last example, let D = a. An annotated clause tree for D is



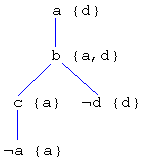
Thus, D' = d. Since d is not evident, a is pertinent.

The above algorithm guarantees finding at least one D' if D is not itself evident. It is not clear at this point whether the algorithm can find D', the set of all D'. Also, is D' merely a means for testing pertinent( D), or is it interesting in and of itself, so that perhaps some D' are preferred over others? Can the algorithm find the D' with the smallest cardinality (a minimal D' ?). Obviously, further investigation is required in this area.

In any event, once pertinent( D) is calculated, Query mode can show the result to the user by displaying the closed clause tree for D|D'. (Unfortunately, there is no satisfactory way of showing that D' is not evident. The best that can be done is to show all the non-closed clause trees for D' -- a rather tedious proposition.) Similarly, Query can show potentially-conflicted( D) by displaying clause trees for D|D' and D|D''.

Refining Query mode

One problem with the current Query mode is that there is no graceful way to stop a running calculation. Recall that Query allows the user to not just verify answers, e.g., evident( a(foo,X)) but generate them, e.g., evident( X) (find all evident terms in the clause database). In either case, there are potentially many solutions and Query mode currently calculates and lists them all. At the very least, it should calculates and lists only n number of solutions (n being small), pauses, and asks the user whether s/he wants to see more. An alternative is to provide a Stop button to interrupt the calculation (although at this point it is not clear how this may be programmed).

Another issue to consider is whether Query should continue to calculate so-called 'global' values for all nodes. Currently, whenever Query displays a clause tree, it calculates all values for all the nodes in the tree. Essentially, it performs a general query on each node. This may slow down the display of trees considerably if the extended meta-logical concepts 'pertinent', 'potentially-conflicted', and 'strongly-conflicted' are added to the query. Fortunately, all these values hinge on generating annotated clause trees (closed or otherwise); therefore, the amount of calculation required can be kept to a minimum by carefully planning the order of calculation and caching the generated results, similar to what the current query engine vl_conflict.pl already does.

Viewing large trees in Query mode

Aside from the ability to expand and collapse branches of the tree, VL currently does not facilitate viewing large trees very well. This section discusses several much-needed improvements in this area. While the focus will be on Query mode, some key ideas presented here are also applicable to Explore mode.

To begin with, a simple improvement would be to not automatically display the entire tree if it is sufficiently large. If there are more than, say, 20 nodes (or some user-definable limit), only the first one or two levels should be displayed. The user can then selectively and incrementally expand nodes and branches as desired. This is probably preferable to displaying the entire tree and forcing the user to collapse branches s/he is not interested in.

Another simple addition would be to exploit XPCE's built-in method tree->zoom <node> which takes any node <node> and treats it as the virtual root of the tree. Only <node> and its children are then visible while the rest of the tree is temporarily hidden. (The tree->unzoom method reverses the effect.) This would be useful for focusing on certain parts of the tree.

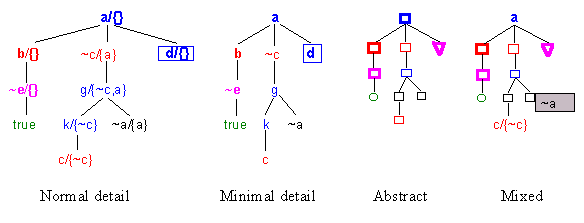
As a major improvement, consider the ability to show tree nodes at different levels of granularity. For example, trees can be displayed in three different detail levels as follows:

• Normal: each node is displayed complete with label (its term) and contingency set. As usual, each node's value is indicated by font size and color. Some graphical convention can be used to indicate whether the node is collapsed (e.g., drawing a box around the node).
• Minimal: same as 'Normal', but display of contingency set is suppressed.
• Abstract: each node is represented only as a graphical icon, such as a small square. (Essentially, 'Abstract' displays the tree as a topological outline.) Each node's value is indicated by the size and color of the icon. A different icon, such as an inverted triangle, can be used to represent a collapsed node.

There should be some mean via the mouse or keyboard or a combination thereof for quickly selecting a detail level or cycling through the three levels. In addition, the user should be able to independently apply the detail level setting to a) all trees in the display, b) a single tree, or c) an individual node. For example, the user may label only a few selected nodes ('minimal') while displaying the rest of the tree in iconic form ('abstract'). Whenever the mouse pointer is placed over the node, a 'Hint' feature will display on the status line information for the node at one detail level greater than its current setting. Hence, the user can temporarily see an 'abstract' node's label by pointing the mouse at the node. Optionally, the user can have the same information displayed in a pop-up 'bubble'.

Below is a sample clause tree at different levels of detail. The right-most tree shows how selected nodes may be shown with more (less) detail than others. Node ~a is iconic but has a pop-up 'bubble' which shows its label. Obviously, the advantage of having different granularity would be more apparent with larger trees whose nodes have longer labels.



Implementing the different levels of visual details should not be unduly difficult, thanks to the object-oriented programming model. Essentially, all that is needed is to add a variable 'granularity' to the tree and node class and modify the method which displays the node so that it renders the node according to said variable. The rest is simply involves responding to user input.

The last proposed enhancement for viewing large trees in Query mode is scaling. With scaling, the user would be able to get a 'bird's eye' view of an entire tree, see a large tree (or a large portion of it) given a small physical screen space, or enlarge portions of the trees that are of interest. In general, scaling can be done in two ways: one is to treat the entire display window or the selected object as a bitmap and perform pixel 'zoom' and 'unzoom' (as done by bitmap-based paint programs); the other is to apply a scaling factor to individual graphical objects or collections of objects (as done by vector-based drawing programs). The second method is preferable in this case since graphicals in VL are already objects, not bitmaps.

Conceivably, the user may select a tree and apply a scaling factor to it using a graphical slider. (Particularly useful would be a "Fit tree to window" command.) The user may also select a portion of a tree by drawing a bounding box around it and then scale just the selection.



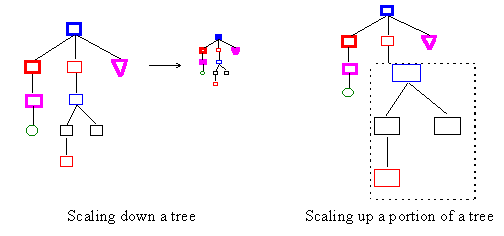
The implementation may be a bit tricky since the current version of XPCE (4.8.14) regrettably does not have a scaling method either for the tree class or device class (in XPCE's terminology, a device is a collection of graphical objects). Therefore, the program would have to apply the scaling to individual objects, including the node connectors, spacing between the nodes, etc. and to make the process transparent so that it appears as if the entire tree object is being scaled. Fortunately, there is a ready demonstration of how this can be done in the sample program pce_draw. Another potential stumbling block is scaling of text images. Unlike other graphical objects, text images in XPCE are bitmaps and do not have a built-in scaling method. Therefore, they would have to be handled in some special way. (How much of a problem they may prove to be is not known at this point.)

Combining all the enhancements discussed above should make viewing large trees much more feasible, thereby significantly improving the usability of the tool as a whole. What's more, the task of implementation should be mostly either straight-forward or doable.