CATEGORY LOGIC
for
- FUNCTOR -
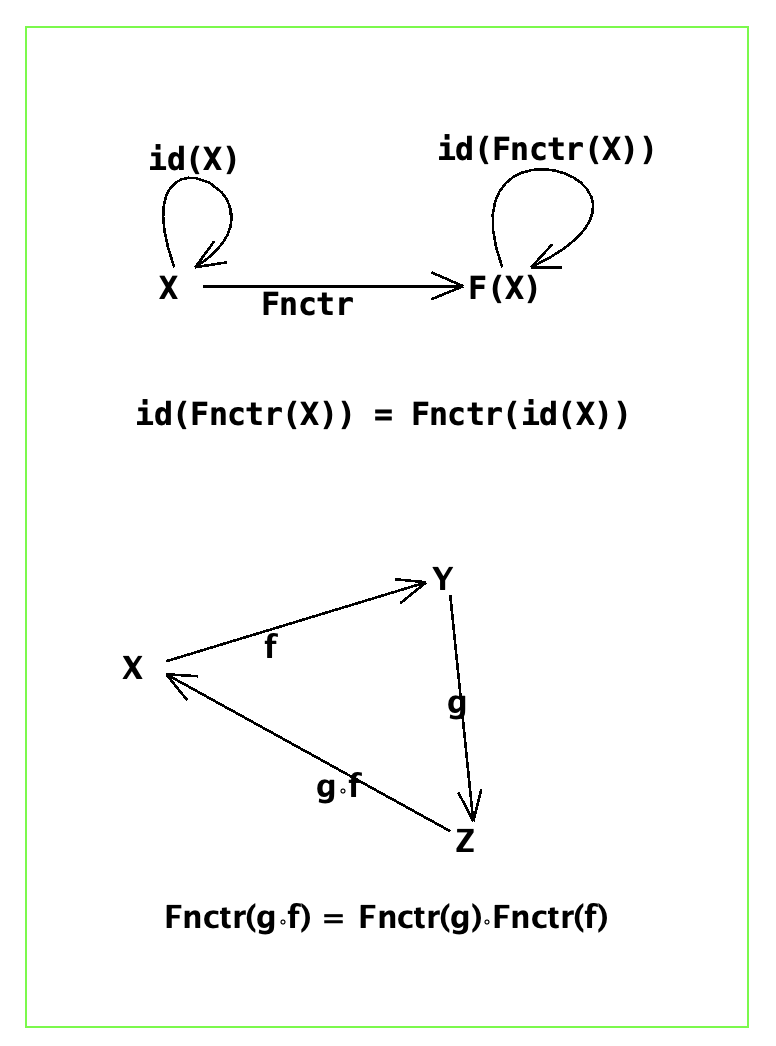
Functor Diagram with Conditions

The (covariant) Functor Diagram above has two sub-diagrams, each having the usual attending
(equality) condition. The translation of the Functor Diagram to an AutoLog theory
is displayed using the following link to the theory (open in new window or tab) :
A pdf file version of the AutoLog source code is linked in order to faithfully display Unicode operator symbols. The pdf first explains the role of the Unicode operator symbols in a comment, followed by the AutoLog source code itself, followed by a comment which displays an inference tree showing a Skolem Machine computation for consequences of the AutoLog source code rules. Regarding the graphical inference tree, the column of numbers to the right indicate which rule number was applied to assert the conclusion in the column on the left. Enlarging the resulting displayed window, and its contents, makes it easier to read more details.
When variables in an antecedent rule literal are matched to earlier facts in the inference tree, those matched values are then available to bind to the corresponding variables in consequent literals. This mechanism is the crux of indexical forcing. The full development of this mechanism is a current task to be included in the Autolog Design Notebook (ADN).
Download the Functor text source code: ↳ Functor.auto
The downloaded text source code file can then be opened using The AUTOLOG app and should compile successfully into the AutoLog Viewer.
Exercise: Use the approach described for Functor to formulate a similar (but more challenging) analysis of category logic for a Natural Transformation. What additional indexical forcing details need to be developed?