Skolem Machines

background information

The following paper introduced the idea of a Skolem Machine for computing coherent logic.

John Fisher and Marc Bezem, Skolem Machines,
Fundamenta Informaticae, 91 (1) 2009, pp.79-103 ↬ SkolemMachines.pdf
The paper also has a ResearchGate page ↬ here

The first link is to a copy of the paper with minor corrections. Note: colog machine code for a Skolem Machine was called geolog in this paper. The paper gives conceptual definitions of a Skolem Machine -- as a tape machine analagous to a Turing Machine and as a tree machine -- and shows that it has theoretical computational universality. The paper does not provide specific implementation design details (e.g. see SAM.pdf link below). Related ↬ papers ...

J. Barkley Rosser: "Of course Turing did it before us. Turing, of course, was awfully concerned with the correct way to do it. 'You do it on a machine, see.' "

colog programming

A colog primer ↬ colog.pdf
Colog is a machine language for a Skolem machine.
Read the primer and use the GUI prover to run the primer's examples (examples/fisher/colog_primer/) ↳ examples.zip.

colog prover

Latest Java implementation ↳ colog14I.jar (made with java version "15.0.1")
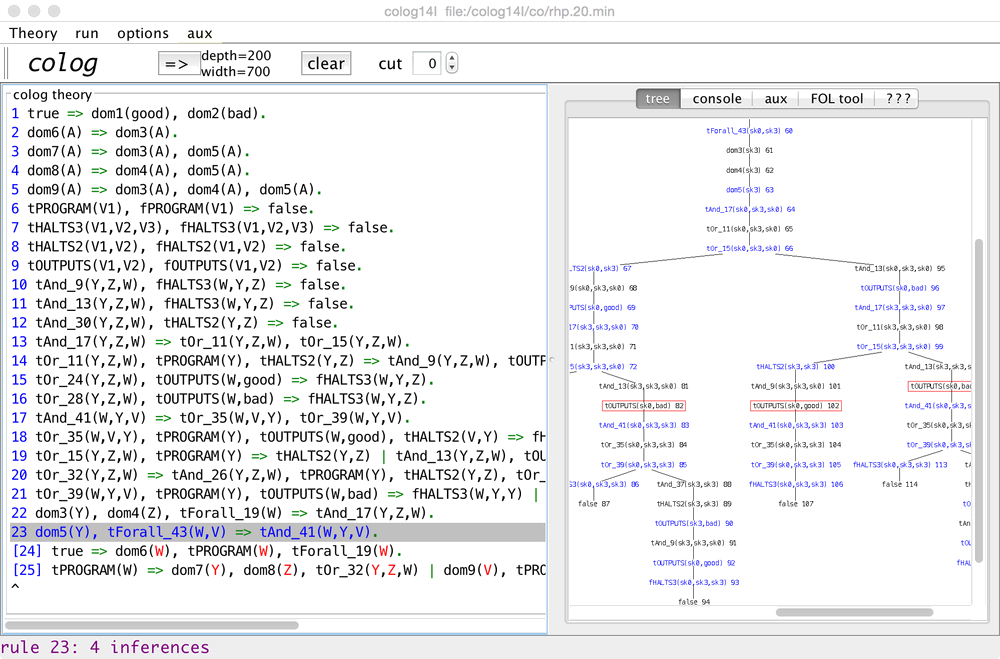
Download the jar, double-click on jar to start the colog proof browser GUI. Read the usage notes under the ??? tab of the proof browser.

Sources: ↳ colog14I.zip (Unzip, See README file)

An old report (2009) describes the fore-and-aft, fol-to-colog translation idea: ↬ fol2cl.pdf. This version of translation is implemented by colog14I (FOL tool tab), and some earlier versions. Various bugs (or difficulties) persist, awaiting new developments.

The colog and FOL parser-generators employed by the prover are implemented using ANTLR grammars.

Constructive Coherent Translation of Propositional Logic, using fore-and-aft Heyting templates ↬ prop2cl.pdf.

Skolem Abstract Machine (SAM) implementation design

Implementation design report for the Skolem Abstract Machine ↬ SAM.pdf
This document outlines design ideas regarding SAM implementation, including the distributive (fair) choices algorithm §5.

Autolog Project

The Autolog Design Notebook (ADN) describes language design and implementation requirements for Autolog, an experimental inference programming system whose implementation employs a conservative extension of the Skolem Abstract Machine. The ADN design elements involve system requirements, autolog implementation code specifications, autolog program code test requirements and test results. The ADN is frequently updated (last post 11/22/2023). Recent developments indicate that more colog14I serial control code needs to be refined and adapted for AutoLog24. This involves new concurrent inference design modifications and testing. There is some delay in getting these design details correctly integrated. The overall effort also requires code design for what is called predicative forcing for indexical rule literals and rule generated active equality rewrites. The Autolog code development README page is here.

---

Autolog Equality Inference, BLAST18, University of Denver ↬ slides.
The slides outline a technique for combining equational reasoning (modulation), algebraic logic and coherent reasoning.

---

Lecture Notes, Autolog Meta Programming
To capture unicode symbols, download and view .txt with AutoLog editor.

#1 - Autolog MetaLogic .pdf .txt
#2 - Autolog Quantifier MetaLogic .pdf .txt
#3 - Autolog Type Metalogic .pdf .txt
#4 - Autolog Category Metalogic .pdf .txt
#5 - Autolog Set Type Metalogic .pdf .txt

The lecture notes describe autolog programs that we would like to compute, along with some suggestions regarding how they should be computed. The examples provide use cases for autolog system code development and testing. A problem is specified using an autolog program. The meaning of the program involves the inference trees that can be generated from the program by a Skolem Machine. The problem answers are specified by the goal rules of the autolog program and inference trees support answers.

---

about category ISOTYPES ‐ categories as type universes

---

11/15/2024 Java IDE
The Java Inference systems (Colog/Autolog) on this page all used a JavApp Interactive Design Environment (IDE) for Java code design and implementation testing. Follow the link to read brief outline description of how the latest version JavApp24 works.

---